四面体 $ABCD$ 的 $ABC$ 面和 $BCD$ 面相交成 $30{}^\circ $ 的角.三角形 $ABC$ 的面积是120,三角形 $BCD$ 的面积是80,且 $BC=10$.试求四面体的体积.
【难度】
【出处】
1992年第10届美国数学邀请赛(AIME)
【标注】
【答案】
320
【解析】
如图所示,设 $H$ 是从点 $D$ 到直线 $BC$ 的垂足.因 $BC=10$,$\vartriangle BCD$ 的面积为80,可知 $DH=16$,再令 $P$ 是从点 $D$ 到平面 $ABC$ 的垂足,易见 $\vartriangle HPD$ 是直角三角形而 $\angle DHP$ 为 $30{}^\circ $.由此可知 $DP=\frac{1}{2}DH=8$.而四面体的体积为 $\frac{1}{3}DP\times {{S}_{\vartriangle ABC}}=\frac{1}{3}\times8\times 120=320$.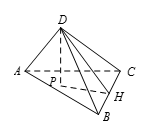

答案
解析
备注