点 $\left( 0, 0 \right)$，$\left( a, 11 \right)$ 和 $\left( b ,37 \right)$ 是一个等边三角形的顶点．求 $a\cdot b$ 的值．
【难度】
【出处】
1994年第12届美国数学邀请赛（AIME）
【标注】
【答案】
315
【解析】
如图所示，设 $O\left( 0 ,0 \right)$，$A\left( a, 11\right)$，$B\left( b, 37 \right)$．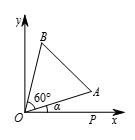
注意到三角形关于 $y$ 轴作反射并不改变 $ab$ 的值．假定从 $\overrightarrow{OA}$ 到 $\overrightarrow{OB}$ 逆时针转的角度为 $60{}^\circ$，且设 $OB=OA=AB=r$，$\angle AOP=\alpha $，其中 $P$ 为 $x$ 轴正方向上一点．$\angle BOP=\alpha +60{}^\circ $．由 $\sin \angle BOP=\sin \alpha \cos 60{}^\circ +\cos \alpha \sin 60{}^\circ $，有 $\frac{37}{r}=\frac{11}{r}\cdot\frac{1}{2}+\frac{a}{r}\cdot \frac{\sqrt{3}}{2}$，得 $a=21\sqrt{3}$．
类似地，$\cos \angle BOP=\cos \alpha \cos 60{}^\circ -\sin \alpha \sin 60{}^\circ $，有 $\frac{b}{r}=\frac{a}{r}\cdot\frac{1}{2}-\frac{11}{r}\cdot \frac{\sqrt{3}}{2}$ 得 $b=5\sqrt{3}$．
所以，$ab=21\sqrt{3}\times5\sqrt{3}=315$．
注意到三角形关于 $y$ 轴作反射并不改变 $ab$ 的值．假定从 $\overrightarrow{OA}$ 到 $\overrightarrow{OB}$ 逆时针转的角度为 $60{}^\circ$，且设 $OB=OA=AB=r$，$\angle AOP=\alpha $，其中 $P$ 为 $x$ 轴正方向上一点．$\angle BOP=\alpha +60{}^\circ $．由 $\sin \angle BOP=\sin \alpha \cos 60{}^\circ +\cos \alpha \sin 60{}^\circ $，有 $\frac{37}{r}=\frac{11}{r}\cdot\frac{1}{2}+\frac{a}{r}\cdot \frac{\sqrt{3}}{2}$，得 $a=21\sqrt{3}$．类似地，$\cos \angle BOP=\cos \alpha \cos 60{}^\circ -\sin \alpha \sin 60{}^\circ $，有 $\frac{b}{r}=\frac{a}{r}\cdot\frac{1}{2}-\frac{11}{r}\cdot \frac{\sqrt{3}}{2}$ 得 $b=5\sqrt{3}$．
所以，$ab=21\sqrt{3}\times5\sqrt{3}=315$．
答案
解析
备注
