如图所示，一束光以入射角 $\alpha =19.94{}^\circ $ 射到线段 $BC$ 的端点 $C$，然后以同样大小的角度反射出去，射到 $AB$ 又继续反射……光绕遵照“入射角等于反射角”的规律在 $AB$ 与 $BC$ 之间反射，若 $\beta =\frac{\alpha }{10}=1.994{}^\circ $，$AB=BC$，且计算中包括第一次由 $C$ 点的反射，试确定光线在两线段之间的反射次数．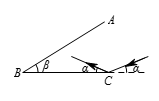
【难度】
【出处】
1994年第12届美国数学邀请赛（AIME）
【标注】
【答案】
71
【解析】
如图所示，光的反射点记为 $C$，${{C}_{1}}$，${{C}_{2}}$，…．作 $B{{D}_{1}}$，使 $B{{D}_{1}}=BC$，且 $\angle CB{{D}_{1}}=\beta $，则 ${{C}_{1}}$ 关于 $BC$ 的对称点为 ${{E}_{1}}$；再作 $B{{D}_{2}}$，使 $\angle{{D}_{1}}B{{D}_{2}}=\beta $，且 $B{{D}_{2}}=B{{D}_{1}}$，则 ${{C}_{2}}$ 关于 $B{{D}_{1}}$ 的对称点为 ${{E}_{2}}$．因为 $\angle C{{E}_{1}}D=\angle {{C}_{2}}{{E}_{1}}B=\angle B{{E}_{1}}{{E}_{2}}$，所以 $C{{E}_{1}}{{E}_{2}}$ 是一条直线．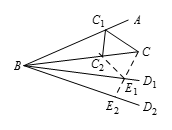
重复上面的过程，作 $B{{D}_{3}}$，$B{{D}_{4}}$，…，其中 $\angle {{D}_{i}}B{{D}_{i+1}}=\beta $．$B{{D}_{i}}=BC$．则得到一条射线 $C{{E}_{1}}$．$BA$ 和 $BC$ 之间的每一个光束反射点都对应于这射线和某 $B{{D}_{i}}$ 的交点 ${{E}_{i}}$．只需计算这些交点个数即可．
如图所示，以 $B$ 为圆心，以 $AB$ 为半径作圆，并作 $\angle BCE=\alpha $，$E$ 为圆上的点，则 $CE$ 与 $B{{D}_{i}}$ 交点 ${{E}_{i}}$ 的个数加1即为所求．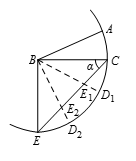
为计算交点 ${{E}_{i}}$ 的个数，首先求 $\angle CBE$．因为 $BE=BC$，则有 $\angle BEC=\angle BCE$．所以 $\angle CBE=180-2\alpha $．因此交点的个数等于 $\left( \frac{180-2\alpha }{\beta } \right)+1$（这里加1是加上第一个反射点 $C$）．
由 $\alpha=19.94{}^\circ $，$\beta =1.994{}^\circ $，我们得到71个交点．即光束在两条线间的反射次数为71．
重复上面的过程，作 $B{{D}_{3}}$，$B{{D}_{4}}$，…，其中 $\angle {{D}_{i}}B{{D}_{i+1}}=\beta $．$B{{D}_{i}}=BC$．则得到一条射线 $C{{E}_{1}}$．$BA$ 和 $BC$ 之间的每一个光束反射点都对应于这射线和某 $B{{D}_{i}}$ 的交点 ${{E}_{i}}$．只需计算这些交点个数即可．如图所示，以 $B$ 为圆心，以 $AB$ 为半径作圆，并作 $\angle BCE=\alpha $，$E$ 为圆上的点，则 $CE$ 与 $B{{D}_{i}}$ 交点 ${{E}_{i}}$ 的个数加1即为所求．
为计算交点 ${{E}_{i}}$ 的个数，首先求 $\angle CBE$．因为 $BE=BC$，则有 $\angle BEC=\angle BCE$．所以 $\angle CBE=180-2\alpha $．因此交点的个数等于 $\left( \frac{180-2\alpha }{\beta } \right)+1$（这里加1是加上第一个反射点 $C$）．由 $\alpha=19.94{}^\circ $，$\beta =1.994{}^\circ $，我们得到71个交点．即光束在两条线间的反射次数为71．
答案
解析
备注
