一个三角形状的纸片 $ABC$ 和其上一点 $P$,考虑将 $A$,$B$,$C$ 折在点 $P$ 上所形成的抓痕,如果三条折痕互不相交,我们称 $P$ 为 $\vartriangle ABC$ 的一个折叠点.如果 $AB=36$,$AC=72$,$\angle B=90{}^\circ $,且由 $\vartriangle ABC$ 折叠点所形成的集合面积具有 $q\text{ }\!\!\pi\!\!\text{ }-r\sqrt{s}$ 的形式,其中 $q$,$r$ 和 $s$ 均为正整数且 $s$ 没有平方因子.求 $q+r+s$.
【难度】
【出处】
1994年第12届美国数学邀请赛(AIME)
【标注】
【答案】
597
【解析】
先来证明 $\vartriangle ABC$ 的折叠点所构成的集合是以 $AB$,$BC$ 为直径的圆的内部的公共部分.
为此需证明,由顶点 $A$ 和 $B$ 折叠在 $P$ 上所形成的抓痕不交的充要条件是 $P$ 位于以 $AB$ 为直径的圆的内部.
事实上.由任一点 $Q$ 折到 $P$ 上所形成的折痕是 $PQ$ 的垂直平分线的一部分.若 $P$ 在以 $AB$ 为直径的圆外,那么 $\vartriangle PAB$ 是锐角三角形,因为 $\angle P$ 是锐角,$\angle PAB$ 和 $\angle PBA$ 分别不超过 $60{}^\circ $ 和 $90{}^\circ $,所以,$\vartriangle PAB$ 的外心在三角形的内部,则折痕相交;若 $P$ 在以 $AB$ 为直径的圆内,那么 $PA$ 和 $PB$ 中垂线交点与 $P$ 被 $AB$ 分开.所以,折痕不在 $\vartriangle ABC$ 内部相交;若 $P$ 在圆上,则折痕在 $AB$ 上相交.
类似地讨论用于以 $BC$ 为直径的圆和以 $AC$ 为直径的圆.
注意到 $\vartriangle ABC$ 的所有内点都在以 $AC$ 为直径的圆内,所以三角形的折叠点所构成的集合是三角形内点和以 $AB$,$BC$ 为直径的圆的内点的公共部分.
下面来求这个公共部分的面积.
如图所示,以 $BC$,$AB$ 为直径的两圆都与 $AC$ 交于 $D$($D$ 是 $B$ 到 $AC$ 的垂足).题目所求的部分是两段圆弧所围的部分.一个是以 $AB$ 中点 $M$ 为圆心,以18为半径的 $120{}^\circ$ 的弧.另一个是以 $BC$ 中点 $N$ 为圆心,以 $18\sqrt{3}$ 为半径的 $60{}^\circ $ 的弧.
则 $\vartriangle DBM$ 和 $\vartriangle DBN$ 的面积分别为 $81\sqrt{3}$ 和 $243\sqrt{3}$,扇形 $DMB$ 和 $DNB$ 的面积分别为 $108\text{ }\!\!\pi\!\!\text{ }$ 和 $162\text{}\!\!\pi\!\!\text{ }$.所求部分的面积是
$\left(108\text{ }\!\!\pi\!\!\text{ }+162\text{ }\!\!\pi\!\!\text{ } \right)-\left(81\sqrt{3}+243\sqrt{3} \right)=270\text{ }\!\!\pi\!\!\text{ }-324\sqrt{3}$.
从而,$q+r+s=270+324+3=597$.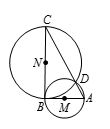
为此需证明,由顶点 $A$ 和 $B$ 折叠在 $P$ 上所形成的抓痕不交的充要条件是 $P$ 位于以 $AB$ 为直径的圆的内部.
事实上.由任一点 $Q$ 折到 $P$ 上所形成的折痕是 $PQ$ 的垂直平分线的一部分.若 $P$ 在以 $AB$ 为直径的圆外,那么 $\vartriangle PAB$ 是锐角三角形,因为 $\angle P$ 是锐角,$\angle PAB$ 和 $\angle PBA$ 分别不超过 $60{}^\circ $ 和 $90{}^\circ $,所以,$\vartriangle PAB$ 的外心在三角形的内部,则折痕相交;若 $P$ 在以 $AB$ 为直径的圆内,那么 $PA$ 和 $PB$ 中垂线交点与 $P$ 被 $AB$ 分开.所以,折痕不在 $\vartriangle ABC$ 内部相交;若 $P$ 在圆上,则折痕在 $AB$ 上相交.
类似地讨论用于以 $BC$ 为直径的圆和以 $AC$ 为直径的圆.
注意到 $\vartriangle ABC$ 的所有内点都在以 $AC$ 为直径的圆内,所以三角形的折叠点所构成的集合是三角形内点和以 $AB$,$BC$ 为直径的圆的内点的公共部分.
下面来求这个公共部分的面积.
如图所示,以 $BC$,$AB$ 为直径的两圆都与 $AC$ 交于 $D$($D$ 是 $B$ 到 $AC$ 的垂足).题目所求的部分是两段圆弧所围的部分.一个是以 $AB$ 中点 $M$ 为圆心,以18为半径的 $120{}^\circ$ 的弧.另一个是以 $BC$ 中点 $N$ 为圆心,以 $18\sqrt{3}$ 为半径的 $60{}^\circ $ 的弧.
则 $\vartriangle DBM$ 和 $\vartriangle DBN$ 的面积分别为 $81\sqrt{3}$ 和 $243\sqrt{3}$,扇形 $DMB$ 和 $DNB$ 的面积分别为 $108\text{ }\!\!\pi\!\!\text{ }$ 和 $162\text{}\!\!\pi\!\!\text{ }$.所求部分的面积是
$\left(108\text{ }\!\!\pi\!\!\text{ }+162\text{ }\!\!\pi\!\!\text{ } \right)-\left(81\sqrt{3}+243\sqrt{3} \right)=270\text{ }\!\!\pi\!\!\text{ }-324\sqrt{3}$.
从而,$q+r+s=270+324+3=597$.

答案
解析
备注