查看数据源：5c6e153f210b281db9f4ca1d
在半径为42的圆中，两条长为78的弦交于一点，该点到圆心的距离为18，两条弦把圆的内部分成4个区域，其中有两块区域的面积相等，并且这两块区域的面积均可以用 $m\text{ }\!\!\pi\!\!\text{ }-n\sqrt{d}$ 的唯一形式表示，其中 $m$，$n$，$d$ 是正整数，且 $d$ 不被任何素数的平方整除，求 $m+n+d$．
【难度】
【出处】
1995年第13届美国数学邀请赛（AIME）
【标注】
  • 知识点
    >
    数论初步
    >
    整除与同余
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的对称性
【答案】
378
【解析】
如图所示，两弦 $AB$，$CD$ 长均为78，所以它们关于过交点 $P$ 的直径 $EF$ 对称．设圆心为 $O$，$AB$ 中点为 $M$，则 $\angle OMA=90{}^\circ $，$OM=\sqrt{O{{A}^{2}}-A{{M}^{2}}}=\sqrt{{{42}^{2}}-{{39}^{2}}}=9\sqrt{3}$．从而 $\operatorname{Rt}\vartriangle OMP$ 中，$\angle OPM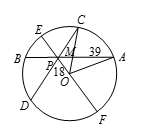=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$．$\angle DPO=\angle OPM=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$，$\angle CPM=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{}}{3}-\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=\frac{\text{ }\!\!\pi\!\!\text{}}{3}$．
$\overset\frown{AC}$ 含角为 $\frac{\text{}\!\!\pi\!\!\text{ }}{3}$，所以弓形 $AC$ 的面积为 ${{S}_{1}}=\frac{1}{2}\times {{42}^{2}}\times \frac{\text{}\!\!\pi\!\!\text{ }}{3}-\frac{\sqrt{3}}{4}\times {{42}^{2}}$，
$m\text{}\!\!\pi\!\!\text{ }-n\sqrt{d}=\frac{1}{2}\times \frac{\sqrt{3}}{2}\times PA\times PC+{{S}_{1}}=\frac{\sqrt{3}}{4}\times PA\times PB+{{S}_{1}}$
$\text{=}\frac{\sqrt{3}}{4}\times PE\times PF+{{S}_{1}}$
$=\frac{\sqrt{3}}{4}\times\left( 42+18 \right)\left( 42-18 \right)+\frac{1}{2}\times {{42}^{2}}\times\frac{\text{ }\!\!\pi\!\!\text{ }}{3}-\frac{\sqrt{3}}{4}\times {{42}^{2}}$
$=294\text{}\!\!\pi\!\!\text{ }-81\sqrt{3}$，
$m+n+d=294+81+3=378$．
答案 解析 备注
0.186879s