一边长为 $1\operatorname{cm}$ 的木制立方体放在一水平面上，在一个上顶点的正上方 $x$ 厘米处的一个点光源照射立方体在水平面上成一影子，这影子的面积，不包括立方体下底面的面积，是 $48{{\operatorname{cm}}^{2}}$．求不超过 $1000x$ 的最大整数．
【难度】
【出处】
1996年第14届美国数学邀请赛（AIME）
【标注】
【答案】
166
【解析】
设 $ABCDEFGH$ 是边长为 $1\operatorname{cm}$ 的正方体，$P$ 是 $E$ 点正上方 $x \operatorname{cm}$ 处的点光源，则 $PE=x$，$EA=1$，如图所示，$P$，$E$，$A$ 共线．$Q$，$R$，$S$ 分别是 $PF$，$PG$，$PH$ 处长线与平面 $ABCD$ 的交点．因为正方形 $EFGH$ 所在平面与正方形 $ABCD$ 所在平面平行，所以棱锥 $PEFGH$ 与棱锥 $PAQRS$ 相似．因此 $AQRS$ 是正方形，并且 $\frac{AQ}{EF}=\frac{AP}{EP}$，即 $\frac{AQ}{1}=\frac{x+1}{x}$．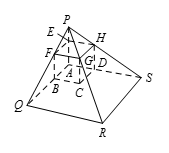
所以 $AQ=\frac{x+1}{x}$．
从而 ${{\left(\frac{x+1}{x} \right)}^{2}}-1=48$，
解之得 $x=\frac{1}{6}$，则 $1000x=\frac{1000}{6}=166\frac{2}{3}$．
故所求最大整数为166．
所以 $AQ=\frac{x+1}{x}$．从而 ${{\left(\frac{x+1}{x} \right)}^{2}}-1=48$，
解之得 $x=\frac{1}{6}$，则 $1000x=\frac{1000}{6}=166\frac{2}{3}$．
故所求最大整数为166．
答案
解析
备注
