在 $\vartriangle ABC$ 中，$AB=\sqrt{30}$，$AC=\sqrt{6}$，$BC=\sqrt{15}$．有一个点 $D$ 使得 $AD$ 平分 $BC$ 并且 $\angle ADB$ 是直角．比值 $\frac{{{S}_{\vartriangle ADB}}}{{{S}_{\vartriangle ABC}}}$ 能写成 $\frac{m}{n}$ 的形式，这里 $m$，$n$ 是互素的正整数．求 $m+n$．
【难度】
【出处】
1996年第14届美国数学邀请赛（AIME）
【标注】
【答案】
65
【解析】
如图所示，设 $BC$ 的中点为 $E$，$AD=\frac{x}{2}$．由中线公式易得 $AE=\frac{\sqrt{57}}{2}$．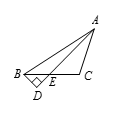
由勾股定理 ${{\left(\sqrt{30} \right)}^{2}}-{{\left( \frac{x}{2} \right)}^{2}}={{\left(\frac{\sqrt{15}}{2} \right)}^{2}}-{{\left( \frac{x}{2}-\frac{\sqrt{57}}{2}\right)}^{2}}$，
即 $120-15+57=2\sqrt{57}x$，
$\frac{m}{n}=\frac{{{S}_{\vartriangle ADB}}}{{{S}_{\vartriangle AEB}}}=\frac{AD}{2AE}=\frac{x}{2\sqrt{57}}=\frac{120-15+57}{4\times57}=\frac{27}{38}$．
故 $m+n=27+38=65$．
由勾股定理 ${{\left(\sqrt{30} \right)}^{2}}-{{\left( \frac{x}{2} \right)}^{2}}={{\left(\frac{\sqrt{15}}{2} \right)}^{2}}-{{\left( \frac{x}{2}-\frac{\sqrt{57}}{2}\right)}^{2}}$，即 $120-15+57=2\sqrt{57}x$，
$\frac{m}{n}=\frac{{{S}_{\vartriangle ADB}}}{{{S}_{\vartriangle AEB}}}=\frac{AD}{2AE}=\frac{x}{2\sqrt{57}}=\frac{120-15+57}{4\times57}=\frac{27}{38}$．
故 $m+n=27+38=65$．
答案
解析
备注
