在平行四边形 $ABCD$ 中，设 $O$ 是对角线 $AC$ 与 $BD$ 的交点．$\angle CAB$ 与 $\angle DBC$ 都是 $\angle DBA$ 的2倍，$\angle ACB$ 是 $\angle AOB$ 的 $r$ 倍．求不超过 $1000r$ 的最大整数．
【难度】
【出处】
1996年第14届美国数学邀请赛（AIME）
【标注】
【答案】
777
【解析】
如图所示，设 $\angle DBA=\alpha $，则 $\angle CAB=\angle CBO=2\alpha $，所以 $\vartriangle CAB\backsim \vartriangle CBO$，
$C{{B}^{2}}=CO\cdot CA=\frac{1}{2}C{{A}^{2}}$．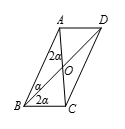
在 $\vartriangle ABC$ 中，由正弦定理得 $\frac{\sin3\alpha }{\sin 2\alpha }=\frac{AC}{BC}=\sqrt{2}$，
即 $3-4{{\sin}^{2}}\alpha =2\sqrt{2}\cos \alpha $．
所以 $4{{\cos }^{2}}\alpha-2\sqrt{2}\cos \alpha -1=0$．
解得 $\cos \alpha=\frac{\sqrt{2}+\sqrt{6}}{4}$，即 $\alpha =15{}^\circ $．于是
$\angle AOB=180{}^\circ -3\times 15{}^\circ =135{}^\circ $
$\angle ACB=135{}^\circ -2\times 15{}^\circ =105{}^\circ $．
所以 $r=\frac{105}{135}=\frac{7}{9}$，则 $1000r=\frac{7000}{9}=777\frac{7}{9}$．
故答案为777．
$C{{B}^{2}}=CO\cdot CA=\frac{1}{2}C{{A}^{2}}$．
在 $\vartriangle ABC$ 中，由正弦定理得 $\frac{\sin3\alpha }{\sin 2\alpha }=\frac{AC}{BC}=\sqrt{2}$，即 $3-4{{\sin}^{2}}\alpha =2\sqrt{2}\cos \alpha $．
所以 $4{{\cos }^{2}}\alpha-2\sqrt{2}\cos \alpha -1=0$．
解得 $\cos \alpha=\frac{\sqrt{2}+\sqrt{6}}{4}$，即 $\alpha =15{}^\circ $．于是
$\angle AOB=180{}^\circ -3\times 15{}^\circ =135{}^\circ $
$\angle ACB=135{}^\circ -2\times 15{}^\circ =105{}^\circ $．
所以 $r=\frac{105}{135}=\frac{7}{9}$，则 $1000r=\frac{7000}{9}=777\frac{7}{9}$．
故答案为777．
答案
解析
备注
