查看数据源：5c6e512b210b287fc7b09645
一辆汽车向正东方向以 $\frac{2}{3}$ 英里/分钟的速度匀速行驶．与此同时，一股半径为51英里的龙卷风，以 $\frac{\sqrt{2}}{2}$ 英里/分钟的速度向东南方向移动．当 $t=0$ 时，龙卷风中心在汽车的正北方110英里处．在 $t={{t}_{1}}$ 时刻，汽车进入了风暴范围．$t={{t}_{2}}$ 时刻，汽车驶出风暴范围．求 $\frac{1}{2}\left( {{t}_{1}}+{{t}_{2}} \right)$．（${{t}_{1}}$，${{t}_{2}}$ 均以分钟计）
【难度】
【出处】
1997年第15届美国数学邀请赛（AIME）
【标注】
  • 知识点
    >
    解析几何
    >
    直线与圆
【答案】
198分钟
【解析】
情形 设 $r$ 为风暴的半径，$d$ 为 $t=0$ 时刻风暴中心与汽车的距离，$c$ 为汽车的速度，则 $\sqrt{2}s$ 为风暴的速度．如图，建立坐标系，使得在 $t=0$ 时刻，风暴中心的坐标为 $\left(0, d \right)$，车在其原始位置并沿 $x$ 轴运动，在任意时刻 $t$，车的位置坐标为 $\left( ct, 0 \right)$，风暴中心位置坐标为 $\left( st, d-st \right)$．当车驶进或开出风暴圈时，这两点间的距离为 $r$，换言之，${{t}_{1}}$，${{t}_{2}}$ 是方程 ${{\left( ct-st \right)}^{2}}+{{\left( d-st \right)}^{2}}={{r}^{2}}$ 的解．此方程可化为 $\left[{{\left( c-s \right)}^{2}}+{{s}^{2}} \right]{{t}^{2}}-\left( 2ds\right)t+\left( {{d}^{2}}-{{r}^{2}} \right)=0$．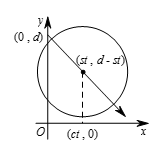由韦达定理得 ${{t}_{1}}+{{t}_{2}}=\frac{2ds}{{{\left(c-s \right)}^{2}}+{{s}^{2}}}$．
现将 $c=\frac{2}{3}$，$d=110$，$s=\frac{1}{2}$ 代入上式得 $\frac{{{t}_{1}}+{{t}_{2}}}{2}=\frac{ds}{{{\left(c-s \right)}^{2}}+{{s}^{2}}}=\frac{110\times \frac{1}{2}}{{{\left(\frac{2}{3}-\frac{1}{2} \right)}^{2}}+{{\left( \frac{1}{2} \right)}^{2}}}=198$．
答案 解析 备注
0.117490s