设笛卡儿平面上的点集 $S$ 满足 $\left| \left| |x \right|-2\left| -1 \right|+\left| \left| |y \right|-2 \right|-1 \right|=1$.若由 $S$ 组成的圆形是由厚度不计的绳子围成的,那么需要绳子的总长为 $a\sqrt{b}$,其中 $a$,$b$ 为正整数,且 $b$ 不能被任意素数的平方整除.求 $a+b$.
【难度】
【出处】
1997年第15届美国数学邀请赛(AIME)
【标注】
【答案】
66
【解析】
利用对称性,在第1象限中画出图形,并将其沿坐标轴翻折.在第1象限中已知方程为
$\left| \left| x-2 \right|-1 \right|+\left|\left| y-2 \right|-1 \right|=1$.
再次利用对称性,在 $x\geqslant 2$,$y\geqslant 2$ 的区域中绘图,并将其沿直线 $x=2$ 及 $y=2$ 翻折,在这个区域内,已知方程进一步化简为 $\left| x-3 \right|+\left| y-3 \right|=1$,
这个方程所表示的图形是一个正方形,其顶点为 $\left(3 ,2 \right)$,$\left( 4 ,3 \right)$,$\left( 3 ,4\right)$ 和 $\left( 2 ,3 \right)$,周长为 $4\sqrt{2}$(图(a)).
沿直线 $x=2$ 及 $y=2$ 的翻折,产生了一系列的正方形,它们的周长为 $4\sqrt{2}\times 4=16\sqrt{2}$,如图(b)所示.沿坐标轴的翻折,又会产生一系列的正方形,它们的总周长为 $4\times 16\sqrt{2}=64\sqrt{2}$,如图(c)所示.因此 $a+b=64+2=66$.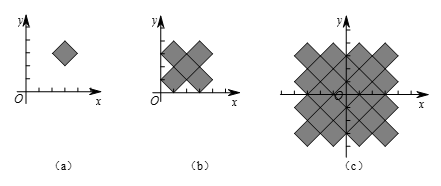
$\left| \left| x-2 \right|-1 \right|+\left|\left| y-2 \right|-1 \right|=1$.
再次利用对称性,在 $x\geqslant 2$,$y\geqslant 2$ 的区域中绘图,并将其沿直线 $x=2$ 及 $y=2$ 翻折,在这个区域内,已知方程进一步化简为 $\left| x-3 \right|+\left| y-3 \right|=1$,
这个方程所表示的图形是一个正方形,其顶点为 $\left(3 ,2 \right)$,$\left( 4 ,3 \right)$,$\left( 3 ,4\right)$ 和 $\left( 2 ,3 \right)$,周长为 $4\sqrt{2}$(图(a)).
沿直线 $x=2$ 及 $y=2$ 的翻折,产生了一系列的正方形,它们的周长为 $4\sqrt{2}\times 4=16\sqrt{2}$,如图(b)所示.沿坐标轴的翻折,又会产生一系列的正方形,它们的总周长为 $4\times 16\sqrt{2}=64\sqrt{2}$,如图(c)所示.因此 $a+b=64+2=66$.

答案
解析
备注