函数 ${{y}^{2}}+2xy+40\left| x \right|=400$ 的图像将坐标平面分成了若干个区域,那么由图像围成的区域的面积是多少?
【难度】
【出处】
1998年第16届美国数学邀请赛(AIME)
【标注】
【答案】
800
【解析】
当 $x\geqslant 0$ 时,由 ${{y}^{2}}+2xy+40\left| x \right|=400$ 得 $\left( y+20\right)\left( y+2x-20 \right)=0$,从而 $y=-20$ 或
$y=-2x+20\left(x\geqslant 0 \right)$;当 $x\leqslant 0$ 时,由 ${{y}^{2}}+2xy+40\left| x \right|=400$ 得 $\left( y-20\right)\left( y+2x+20 \right)=0$,从而 $y=20$ 或 $y=-2x-20\left( x\leqslant 0 \right)$(如图).故由 ${{y}^{2}}-2xy+40\left|x \right|=400$ 围出的区域是一个底为20,高为40的平行四边形,其面积为800.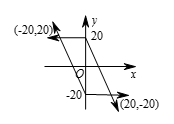
$y=-2x+20\left(x\geqslant 0 \right)$;当 $x\leqslant 0$ 时,由 ${{y}^{2}}+2xy+40\left| x \right|=400$ 得 $\left( y-20\right)\left( y+2x+20 \right)=0$,从而 $y=20$ 或 $y=-2x-20\left( x\leqslant 0 \right)$(如图).故由 ${{y}^{2}}-2xy+40\left|x \right|=400$ 围出的区域是一个底为20,高为40的平行四边形,其面积为800.

答案
解析
备注