设 $ABCD$ 是一个平行四边形,延长 $DA$ 至 $P$,$PC$ 交 $AB$ 于 $Q$,交 $DB$ 于 $R$.已知 $PQ=735$,$QR=112$,求 $RC$.
【难度】
【出处】
1998年第16届美国数学邀请赛(AIME)
【标注】
【答案】
308
【解析】
如图所示,设 $RC=x$,则 $\frac{QB}{CD}=\frac{112}{x}$,由于 $CD=AB$,故 $\frac{QB}{AB}=\frac{112}{x}$.
又因为 $\frac{BQ}{AQ}=\frac{QC}{QP}=\frac{112+x}{735}$,从而 $\frac{QB}{AB}=\frac{112+x}{847+x}$,故 $\frac{112}{x}=\frac{112+x}{847+x}$,
解得 $x=\sqrt{112\times847}=308$,因此 $RC=308$.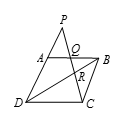
又因为 $\frac{BQ}{AQ}=\frac{QC}{QP}=\frac{112+x}{735}$,从而 $\frac{QB}{AB}=\frac{112+x}{847+x}$,故 $\frac{112}{x}=\frac{112+x}{847+x}$,
解得 $x=\sqrt{112\times847}=308$,因此 $RC=308$.

答案
解析
备注