设 $\vartriangle ABC$ 为等边三角形，$D$，$E$，$F$ 分别为边 $CB$，$CA$，$AB$ 的中点．点 $P$，$Q$，$R$ 分别在 $DE$，$EF$ 和 $FD$ 上，点 $P$，$Q$，$R$ 分别在 $CQ$，$AR$，$BP$ 上．若 $\frac{{{S}_{\vartriangle ABC}}}{{{S}_{\vartriangle PQR}}}=a+b\sqrt{c}$，其中 $a$，$b$，$c$ 为整数，$c$ 不能被任何素数的平方整除．求 ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}$．
【难度】
【出处】
1998年第16届美国数学邀请赛（AIME）
【标注】
【答案】
83
【解析】
如图所示，设 $\vartriangle ABC$ 边长为2，$FQ=x$，则 $EQ=1-x$，由于 $\frac{FQ}{EQ}=\frac{FR}{AE}$，故 $FR=\frac{x}{1-x}$，$DR=1-FR=\frac{1-2x}{1-x}$，同理，由 $\frac{DP}{FB}=\frac{DR}{FR}$，得 $DP=\frac{1-2x}{x}$，$EP=1-DP=\frac{3x-1}{x}$，又由 $\frac{EP}{PD}=\frac{EQ}{CD}$ 知 $1-x=\frac{3x-1}{1-2x}$．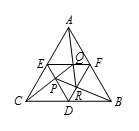
从而 $x=\frac{3-\sqrt{5}}{2}$，于是
$Q{{R}^{2}}=Q{{F}^{2}}+F{{R}^{2}}-FQ\cdot FR$
$={{\left( \frac{3-\sqrt{5}}{2} \right)}^{2}}+{{\left(\frac{\sqrt{5}-1}{2} \right)}^{2}}-\frac{3-\sqrt{5}}{2}\cdot\frac{\sqrt{5}-1}{2}$
$=7-3\sqrt{5}$．
同理可知，$P{{R}^{2}}=P{{Q}^{2}}=7-3\sqrt{5}$，故 $\vartriangle PQR$ 为正三角形，从而
$\frac{{{S}_{\vartriangle ABC}}}{{{S}_{\vartriangle PQR}}}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}=\frac{4}{7-3\sqrt{5}}=7+3\sqrt{5}$．
故 ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}={{7}^{2}}+{{3}^{2}}+{{5}^{2}}=83$．
从而 $x=\frac{3-\sqrt{5}}{2}$，于是$Q{{R}^{2}}=Q{{F}^{2}}+F{{R}^{2}}-FQ\cdot FR$
$={{\left( \frac{3-\sqrt{5}}{2} \right)}^{2}}+{{\left(\frac{\sqrt{5}-1}{2} \right)}^{2}}-\frac{3-\sqrt{5}}{2}\cdot\frac{\sqrt{5}-1}{2}$
$=7-3\sqrt{5}$．
同理可知，$P{{R}^{2}}=P{{Q}^{2}}=7-3\sqrt{5}$，故 $\vartriangle PQR$ 为正三角形，从而
$\frac{{{S}_{\vartriangle ABC}}}{{{S}_{\vartriangle PQR}}}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}=\frac{4}{7-3\sqrt{5}}=7+3\sqrt{5}$．
故 ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}={{7}^{2}}+{{3}^{2}}+{{5}^{2}}=83$．
答案
解析
备注
