正方体的三条棱的 $AB$,$BC$ 和 $CD$,$AD$ 是体对角线.点 $P$,$Q$,$R$ 分别在 $AB$,$BC$,$CD$ 上,$AP=5$,$PB=15$,$BQ=15$,$CR=10$.那么,平面 $PQR$ 向各方向延伸后与正方体的交线组成的多边形的面积是多少?
【难度】
【出处】
1998年第16届美国数学邀请赛(AIME)
【标注】
【答案】
525
【解析】
如图所示,因为 $BP=BQ$,所以 $PQ\parallel AC$,这样过 $R$ 的平行于 $PQ$ 的直线交 $AF$ 于 $U$ 且 $AU=CR$.因为过 $R$ 且平行于 $PQ$ 的直线在平面 $PQR$ 上,所以 $U$ 是相交得出的多边形的顶点,又 $RU$ 的中点是正方体的中心,故相交得出的多边形上的点关于正方体中心对称,因此它的面积是梯形 $PQRU$ 的面积的两倍,梯形 $PQRU$ 的高为 $\sqrt{U{{P}^{2}}-{{\left( \frac{UR-PQ}{2} \right)}^{2}}}$.
又易知 $UR=20\sqrt{2}$,$PQ=15\sqrt{2}$,$UP=\sqrt{125}$,故所求面积为
$\left(UR+PQ \right)\sqrt{U{{P}^{2}}-{{\left( \frac{UP-PQ}{2}\right)}^{2}}}=3\sqrt{2}\sqrt{\frac{225}{2}}=525$.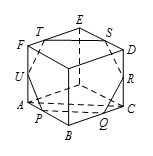
又易知 $UR=20\sqrt{2}$,$PQ=15\sqrt{2}$,$UP=\sqrt{125}$,故所求面积为
$\left(UR+PQ \right)\sqrt{U{{P}^{2}}-{{\left( \frac{UP-PQ}{2}\right)}^{2}}}=3\sqrt{2}\sqrt{\frac{225}{2}}=525$.

答案
解析
备注