平行四边形的顶点坐标为 $\left( 10,45 \right)$，$\left( 10,114 \right)$，$\left( 28,153 \right)$ 和 $\left( 28,84 \right)$．一条通过原点的直线将此平行四边形分成两个全等的多边形，此直线的斜率为 $\frac{m}{n}$，其中 $m$，$n$ 为互素的正整数．求 $m+n$ 的值．
【难度】
【出处】
1999年第17届美国数学邀请赛（AIME）
【标注】
【答案】
118
【解析】
首先证明，平分平行四边形面积的直线必过该平行四边形的中心，事实上，该直线必与平行四边形的一组对边相交，否则该直线就不能平分平行四边形的面积．如图所示，设 $l$ 与平行四边形 $ABCD$ 的一组对边 $AB$，$CD$ 交于 $E$，$F$，设 $CD$ 边上的高为 $h$，于是由 ${{S}_{AEFD}}={{S}_{EBCF}}$ 知
$\frac{1}{2}\left(AE+DF \right)h=\frac{1}{2}\left( BE+CF \right)h$．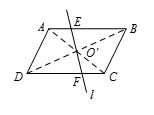
故 $AE+DF=BE+CF$，又 $AE+BE=DF+CF$，从而 $AE=CF$，故 $EF$，即 $l$ 过四边形 $ABCD$ 的中心．
回到原命题，由于通过原点的直线将平行四边形分成两个全等的多边形，从而该直线必过平行四边形的中心 $\left( \frac{10+28}{2}, \frac{45+153}{2} \right)$，即 $\left( 19, 99 \right)$，故 $\frac{m}{n}=\frac{99}{19}$，从而 $m+n=99+19=118$．
$\frac{1}{2}\left(AE+DF \right)h=\frac{1}{2}\left( BE+CF \right)h$．
故 $AE+DF=BE+CF$，又 $AE+BE=DF+CF$，从而 $AE=CF$，故 $EF$，即 $l$ 过四边形 $ABCD$ 的中心．回到原命题，由于通过原点的直线将平行四边形分成两个全等的多边形，从而该直线必过平行四边形的中心 $\left( \frac{10+28}{2}, \frac{45+153}{2} \right)$，即 $\left( 19, 99 \right)$，故 $\frac{m}{n}=\frac{99}{19}$，从而 $m+n=99+19=118$．
答案
解析
备注
