第一象限坐标平面上的一个变换使得每个点 $\left( x ,y \right)$ 映射成为 $\left( \sqrt{x} ,\sqrt{y} \right)$．四边形 $ABCD$ 各顶点的坐标为 $A\left( 900, 300 \right)$，$B\left( 1800, 600 \right)$，$C\left( 600, 1800 \right)$，$D\left( 300 ,900 \right)$．用 $k$ 表示四边形 $ABCD$ 的映象所围成的图形的面积．求不超过 $k$ 的最大整数．
【难度】
【出处】
1999年第17届美国数学邀请赛（AIME）
【标注】
【答案】
314
【解析】
由题意，如图所示，$A$，$B$，$C$，$D$ 4点的像分别为 ${A}'\left(30,10\sqrt{3} \right)$，${B}'\left( 30\sqrt{2},10\sqrt{6} \right)$，${C}'\left( 10\sqrt{6},30\sqrt{2} \right)$，${D}'\left( 10\sqrt{3},30 \right)$ 由于线段 $AB$ 上每一点 $\left(x y \right)$ 满足 $\frac{y}{x}=\frac{\sqrt{3}}{3}$，故其映象在 $y=\frac{\sqrt{3}}{3}x$ 上，从而线段 $AB$ 的映象为线段 ${A}'{B}'$，同理线段 $CD$ 的映象为线段 ${C}'{D}'$．又因为线段 $AD$ 上一点 $\left( x,y \right)$ 满足 $x+y=1200$，故其映象在 ${{x}^{2}}+{{y}^{2}}=1200$ 上，从而线段 $AD$ 的映象为圆弧 ${{x}^{2}}+{{y}^{2}}=1200\left(10\sqrt{3}\leqslant x\leqslant 30 \right)$，同理线段 $BC$ 的映象为圆弧 ${{x}^{2}}+{{y}^{2}}=2400\left(10\sqrt{6}\leqslant x\leqslant 30\sqrt{2} \right)$．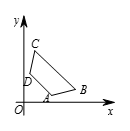
如图所示，由 ${{l}_{1}}$，${{l}_{2}}$ 斜率分别为 $\frac{\sqrt{3}}{3}$，$\sqrt{3}$，从而 ${{l}_{1}}$ 与 ${{l}_{2}}$ 夹角 $\theta=30{}^\circ $，
故 $k={{S}_{{A}'{B}'{C}'{D}'}}=\frac{1}{2}\cdot\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\left( 2400-1200 \right)=100\text{}\!\!\pi\!\!\text{ }$，
从而 $\left[ k\right]=\left[ 100\text{ }\!\!\pi\!\!\text{ } \right]=314$．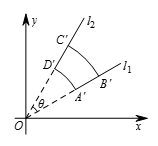
如图所示，由 ${{l}_{1}}$，${{l}_{2}}$ 斜率分别为 $\frac{\sqrt{3}}{3}$，$\sqrt{3}$，从而 ${{l}_{1}}$ 与 ${{l}_{2}}$ 夹角 $\theta=30{}^\circ $，故 $k={{S}_{{A}'{B}'{C}'{D}'}}=\frac{1}{2}\cdot\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\left( 2400-1200 \right)=100\text{}\!\!\pi\!\!\text{ }$，
从而 $\left[ k\right]=\left[ 100\text{ }\!\!\pi\!\!\text{ } \right]=314$．
答案
解析
备注
