设 $T$ 为位于平面 $x+y+z=1$ 上的三元有序实数组 $\left( x, y, z \right)$ 的集合,其中 $x ,y ,z\geqslant 0$.当 $x\geqslant a$,$y\geqslant b$,$z\geqslant c$ 中恰有两个成立时,我们称 $\left( x ,y ,z \right)$ 支撑 $\left( a, b, c \right)$.令 $S$ 为 $T$ 中支撑 $\left( \frac{1}{2} ,\frac{1}{3}, \frac{1}{6} \right)$ 的三元组组成的集合,$S$,$T$ 的面积比为 $\frac{m}{n}$,其中 $m$,$n$ 为互素的正整数,求 $m+n$.
【难度】
【出处】
1999年第17届美国数学邀请赛(AIME)
【标注】
【答案】
25
【解析】
$T$ 是第一卦限内的等边三角形,其顶点坐标分别为 $\left(1 0 0 \right)$,$\left( 0 ,1 ,0 \right)$,$\left( 0, 0 ,1\right)$.平面 $x=\frac{1}{2}$,$y=\frac{1}{3}$,$z=\frac{1}{6}$ 与平面 $x+y+z=1$ 的交线分别与 $T$ 的三边平行,如图所示.令 $A$ 表示 $T$ 中满足 $x\geqslant\frac{1}{2}$ 且 $y\geqslant \frac{1}{3}$ 的点的集合.注意到 $A$ 中各点满足 $z\geqslant\frac{1}{6}$,故 $A$ 中的点支撑 $\left( \frac{1}{2} ,\frac{1}{3} ,\frac{1}{6} \right)$(除去点 $\left(\frac{1}{2} ,\frac{1}{3} ,\frac{1}{6} \right)$ 本身).同理,令 $B$ 表示 $T$ 中满足 $x\geqslant\frac{1}{2}$ 且 $z\geqslant \frac{1}{6}$ 的点组成的集合,除点 $\left(\frac{1}{2} ,\frac{1}{3} ,\frac{1}{6} \right)$ 之外,令 $C$ 表示 $T$ 中满足 $y\geqslant\frac{1}{3}$ 且 $z\geqslant \frac{1}{6}$ 的点组成的集合.除点 $\left(\frac{1}{2} ,\frac{1}{3}, \frac{1}{6} \right)$ 之外,$S$ 是等边三角形 $A$,$B$,$C$ 的并.又三角形 $A$,$B$,$C$ 各边长分别是三角形 $T$ 各边长的 $\frac{1}{6}$,$\frac{1}{3}$ 和 $\frac{1}{2}$,故它们的面积分别是三角形 $T$ 的面积的 $\frac{1}{36}$,$\frac{1}{9}$ 和 $\frac{1}{4}$.从而 $S$ 的面积与 $T$ 的面积比为 $\frac{1}{36}+\frac{1}{9}+\frac{1}{4}=\frac{7}{18}$.故 $m+n=25$.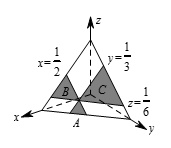

答案
解析
备注