坐标纸上一个三角形顶点的坐标分别为 $\left( 0,0 \right)$,$\left( 34,0 \right)$ 及 $\left( 16,24 \right)$,它的中点三角形的顶点是其各边的中点,沿这个中点三角形的三边将大三角形折起形成一个三棱锥.问该三棱锥的体积是多大?
【难度】
【出处】
1999年第17届美国数学邀请赛(AIME)
【标注】
【答案】
408
【解析】
如图所示,设折成的三棱锥的4个顶点为 $A$,$B$,$C$,$D$,原坐标纸上的三角形三边长为 $a$,$b$,$c$,故不妨设 $AB=CD=\frac{a}{2}$,$AD=BC=\frac{b}{2}$,$AC=BD=\frac{c}{2}$.将四面体 $ABCD$ 看成由一个长、宽、高分别为 $x$,$y$,$z$ 的长方体切去4个直三棱锥得到,从而 ${{V}_{ABCD}}=xyz-\frac{1}{6}xyz\times4=\frac{1}{3}xyz$.
因为 ${{x}^{2}}+{{y}^{2}}=\frac{1}{4}{{a}^{2}}$,${{y}^{2}}+{{z}^{2}}=\frac{1}{4}{{b}^{2}}$,${{z}^{2}}+{{x}^{2}}=\frac{1}{4}{{c}^{2}}$,
所以 ${{x}^{2}}{{y}^{2}}{{z}^{2}}=\frac{1}{512}\left({{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)\left( {{a}^{2}}+{{c}^{2}}-{{b}^{2}}\right)\left( {{b}^{2}}+{{c}^{2}}-{{a}^{2}} \right)$
$=\frac{1}{512}\left[ {{34}^{2}}+\left({{16}^{2}}+{{24}^{2}} \right)-\left( {{18}^{2}}+{{24}^{2}} \right)\right]\left[ {{34}^{2}}+\left( {{18}^{2}}+{{24}^{2}} \right) \right.$
$\left. -\left( {{16}^{2}}+{{24}^{2}}\right) \right]\left[ \left( {{18}^{2}}+{{24}^{2}} \right)+\left({{16}^{2}}+{{24}^{2}} \right)-{{34}^{2}} \right]$
$={{1224}^{2}}$
所以三棱锥体积为 $\frac{1}{3}xyz=\frac{1}{3}\times1224=408$.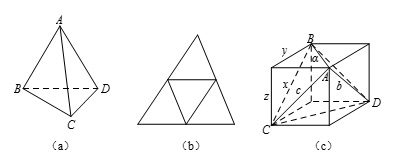
因为 ${{x}^{2}}+{{y}^{2}}=\frac{1}{4}{{a}^{2}}$,${{y}^{2}}+{{z}^{2}}=\frac{1}{4}{{b}^{2}}$,${{z}^{2}}+{{x}^{2}}=\frac{1}{4}{{c}^{2}}$,
所以 ${{x}^{2}}{{y}^{2}}{{z}^{2}}=\frac{1}{512}\left({{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)\left( {{a}^{2}}+{{c}^{2}}-{{b}^{2}}\right)\left( {{b}^{2}}+{{c}^{2}}-{{a}^{2}} \right)$
$=\frac{1}{512}\left[ {{34}^{2}}+\left({{16}^{2}}+{{24}^{2}} \right)-\left( {{18}^{2}}+{{24}^{2}} \right)\right]\left[ {{34}^{2}}+\left( {{18}^{2}}+{{24}^{2}} \right) \right.$
$\left. -\left( {{16}^{2}}+{{24}^{2}}\right) \right]\left[ \left( {{18}^{2}}+{{24}^{2}} \right)+\left({{16}^{2}}+{{24}^{2}} \right)-{{34}^{2}} \right]$
$={{1224}^{2}}$
所以三棱锥体积为 $\frac{1}{3}xyz=\frac{1}{3}\times1224=408$.

答案
解析
备注