一个直立圆锥形容器高12英寸，底面圆半径为5英寸．当该容器顶朝下，底面水平时，密封在里面的液体高9英寸．当容器顶朝上，底面水平时，液体高 $m-n\sqrt[3]{p}$ 英寸，其中 $m$，$n$，$p$ 均为正整数且 $p$ 不能被任何素数的立方整除．求 $m+n+p$．
【难度】
【出处】
2000年第18届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
52
【解析】
由图（a）知，容器中液体体积 $V=\frac{1}{3}\text{}\!\!\pi\!\!\text{ }\cdot {{5}^{2}}\cdot 12\cdot {{\left( \frac{9}{12}\right)}^{3}}=\frac{25\cdot 27}{16}\text{ }\!\!\pi\!\!\text{ }$．
在图（b）中，设液体高为 $h$ 英寸，上底面半径为 $r$ 英寸，于是 $\frac{12-h}{12}=\frac{r}{5}$，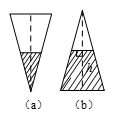
从而 $r=\frac{5\left(12-h \right)}{12}$，故
$V=\frac{1}{3}\text{}\!\!\pi\!\!\text{ }h\left( {{r}^{2}}+5r+25 \right)$
$=\frac{1}{3}\text{ }\!\!\pi\!\!\text{}h\left( \frac{25{{\left( 12-h \right)}^{2}}}{{{12}^{2}}}+\frac{25\left( 12-h\right)}{12}+25 \right)$
$=\frac{25}{432}\text{ }\!\!\pi\!\!\text{}h\left( {{h}^{2}}-36h+432 \right)$
$=\frac{25}{432}\text{ }\!\!\pi\!\!\text{}\left[ {{\left( h-12 \right)}^{3}}+{{12}^{3}} \right]$．
又由 $V=\frac{25\cdot27}{16}\text{ }\!\!\pi\!\!\text{ }$ 知 $\frac{25\cdot27}{16}\text{ }\!\!\pi\!\!\text{ }=\frac{25}{432}\text{ }\!\!\pi\!\!\text{}\left[ {{\left( h-12 \right)}^{3}}+{{12}^{3}} \right]$，
即 ${{\left( 12-h\right)}^{3}}={{12}^{3}}-{{27}^{2}}=999$．
故 $12-h=3\sqrt[3]{37}$，从而 $h=12-3\sqrt[3]{37}$．
因此 $m+n+p=12+3+37=52$．
在图（b）中，设液体高为 $h$ 英寸，上底面半径为 $r$ 英寸，于是 $\frac{12-h}{12}=\frac{r}{5}$，
从而 $r=\frac{5\left(12-h \right)}{12}$，故$V=\frac{1}{3}\text{}\!\!\pi\!\!\text{ }h\left( {{r}^{2}}+5r+25 \right)$
$=\frac{1}{3}\text{ }\!\!\pi\!\!\text{}h\left( \frac{25{{\left( 12-h \right)}^{2}}}{{{12}^{2}}}+\frac{25\left( 12-h\right)}{12}+25 \right)$
$=\frac{25}{432}\text{ }\!\!\pi\!\!\text{}h\left( {{h}^{2}}-36h+432 \right)$
$=\frac{25}{432}\text{ }\!\!\pi\!\!\text{}\left[ {{\left( h-12 \right)}^{3}}+{{12}^{3}} \right]$．
又由 $V=\frac{25\cdot27}{16}\text{ }\!\!\pi\!\!\text{ }$ 知 $\frac{25\cdot27}{16}\text{ }\!\!\pi\!\!\text{ }=\frac{25}{432}\text{ }\!\!\pi\!\!\text{}\left[ {{\left( h-12 \right)}^{3}}+{{12}^{3}} \right]$，
即 ${{\left( 12-h\right)}^{3}}={{12}^{3}}-{{27}^{2}}=999$．
故 $12-h=3\sqrt[3]{37}$，从而 $h=12-3\sqrt[3]{37}$．
因此 $m+n+p=12+3+37=52$．
答案
解析
备注
