大草原的中央,一辆消防车停在相互垂直的两条高速公路程的交叉处,此消防车以每小时50英里的速度沿高速公路程行驶,以每小时14英里的速度横穿草原,由该车在6分钟内能到达的地点所围成的图形的面积为 $\frac{m}{n}$ 平方英里,这里 $m$,$n$ 为互素的正整数.求 $m+n$.
【难度】
【出处】
2000年第18届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
731
【解析】
设消防车在高速公路上行驶的时间为 $t$ 小时,其中 $0\leqslant t\leqslant \frac{1}{10}$,于是汽车在6分钟内能到达的地点构成的集合为以 $\left( 0, \pm 50t \right)$ 或 $\left( \pm 50 t,0 \right)$ 为圆心,$14\left( \frac{1}{10}-t \right)$ 为半径的圆周及其内部的点构成集合的并集,其中 $t$ 取遍 $\left[ 0, \frac{1}{10} \right]$ 中的数.
过 $A\left( 0 ,5\right)$ 作圆 ${{x}^{2}}+{{y}^{2}}={{\left( 1.4 \right)}^{2}}$ 的切线 ${{l}_{1}}$ 与 ${{l}_{2}}$,对于圆心为 $\left(0 ,50t \right)$,半径为 $14\left( \frac{1}{10}-t \right)$ 的圆,由于 $\frac{14\left(\frac{1}{10}-t \right)}{5-50t}=\frac{14}{50}$.从而该也与 ${{l}_{1}}$ 与 ${{l}_{2}}$ 相切.故易知围成的图形为“四角星”$A{{A}_{1}}B{{B}_{1}}C{{C}_{1}}D{{D}_{1}}$.
如图所示,由于 $AF$ 与 ${{x}^{2}}+{{y}^{2}}={{\left(1.4 \right)}^{2}}$ 相切,故 $\sin \alpha =\frac{1.4}{5}=\frac{7}{25}$,
从而 $\tan \alpha=\frac{7}{24}$,于是 $OF=5\times \frac{7}{24}=\frac{35}{24}$.
同理 $OE=\frac{35}{24}$.
从而 $\frac{{{S}_{\vartriangle{{A}_{1}}BO}}}{{{S}_{\vartriangle A{{A}_{1}}B}}}=\frac{OE}{EA}=\frac{7}{17}=\frac{OF}{BF}=\frac{{{S}_{\vartriangle{{A}_{1}}AO}}}{{{S}_{\vartriangle A{{A}_{1}}B}}}$.
故 ${{S}_{A{{A}_{1}}BO}}\text{=}\frac{14}{31}$,${{S}_{\vartriangle ABO}}\text{=}\frac{7}{31}\cdot {{5}^{2}}\text{=}\frac{175}{31}$.
因此“四角星”的面积为 $\frac{175}{31}\times4=\frac{700}{31}$,故 $m+n=731$.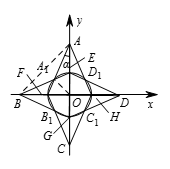
过 $A\left( 0 ,5\right)$ 作圆 ${{x}^{2}}+{{y}^{2}}={{\left( 1.4 \right)}^{2}}$ 的切线 ${{l}_{1}}$ 与 ${{l}_{2}}$,对于圆心为 $\left(0 ,50t \right)$,半径为 $14\left( \frac{1}{10}-t \right)$ 的圆,由于 $\frac{14\left(\frac{1}{10}-t \right)}{5-50t}=\frac{14}{50}$.从而该也与 ${{l}_{1}}$ 与 ${{l}_{2}}$ 相切.故易知围成的图形为“四角星”$A{{A}_{1}}B{{B}_{1}}C{{C}_{1}}D{{D}_{1}}$.
如图所示,由于 $AF$ 与 ${{x}^{2}}+{{y}^{2}}={{\left(1.4 \right)}^{2}}$ 相切,故 $\sin \alpha =\frac{1.4}{5}=\frac{7}{25}$,
从而 $\tan \alpha=\frac{7}{24}$,于是 $OF=5\times \frac{7}{24}=\frac{35}{24}$.
同理 $OE=\frac{35}{24}$.
从而 $\frac{{{S}_{\vartriangle{{A}_{1}}BO}}}{{{S}_{\vartriangle A{{A}_{1}}B}}}=\frac{OE}{EA}=\frac{7}{17}=\frac{OF}{BF}=\frac{{{S}_{\vartriangle{{A}_{1}}AO}}}{{{S}_{\vartriangle A{{A}_{1}}B}}}$.
故 ${{S}_{A{{A}_{1}}BO}}\text{=}\frac{14}{31}$,${{S}_{\vartriangle ABO}}\text{=}\frac{7}{31}\cdot {{5}^{2}}\text{=}\frac{175}{31}$.
因此“四角星”的面积为 $\frac{175}{31}\times4=\frac{700}{31}$,故 $m+n=731$.

答案
解析
备注