在 $\vartriangle ABC$ 中，已知 $\angle B$ 和 $\angle C$ 相等．点 $P$，$Q$ 分别在 $AC$ 和 $AB$ 上，使得 $AP=PQ=QB=BC$．$\angle ACB$ 是 $\angle APQ$ 的 $r$ 倍，其中 $r$ 是正实数，求不超过 $1000r$ 的最大整数．
【难度】
【出处】
2000年第18届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
571
【解析】
如图所示，$x$ 表示 $\angle QPB$．由于 $\angle AQP$ 是等腰三角形 $BQP$ 的一个外角，故 $\angle AQP=2x$，且 $\angle PAQ=2x$．
由于 $\angle BPC$ 是 $\vartriangle BPA$ 的一个外角，则 $\angle BPC=3x$．
令 $\angle PBC=y$，则有 $\angle ACB=x+y$，且 $4x+2y=180$．
又 $\vartriangle APQ$ 有两个内角均为 $2x$，则 $\angle APQ=2y$，于是 $AQ=2\cdot AP\cdot \sin y$．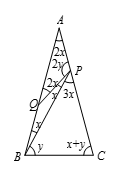
又 $AB=AC$，且 $AP=QB$，所以 $AQ=PC$．
对 $\vartriangle PBC$ 运用正弦定理有 $\frac{\sin3x}{BC}=\frac{\sin y}{PC}=\frac{\sin y}{2\cdot AP\cdot \sin y}=\frac{1}{2\cdot AP}$．
又 $AP=BC$，推出 $\sin3x=\frac{1}{2}$；
$4x<180$，推出 $3x=30$，所以 $x=10$．
故 $y=70$，$r=\frac{10+70}{2\cdot70}=\frac{4}{7}$．
因此求出 $1000r=571+\frac{3}{7}$．
故 $\left[ 1000r\right]=571$．
由于 $\angle BPC$ 是 $\vartriangle BPA$ 的一个外角，则 $\angle BPC=3x$．
令 $\angle PBC=y$，则有 $\angle ACB=x+y$，且 $4x+2y=180$．
又 $\vartriangle APQ$ 有两个内角均为 $2x$，则 $\angle APQ=2y$，于是 $AQ=2\cdot AP\cdot \sin y$．
又 $AB=AC$，且 $AP=QB$，所以 $AQ=PC$．对 $\vartriangle PBC$ 运用正弦定理有 $\frac{\sin3x}{BC}=\frac{\sin y}{PC}=\frac{\sin y}{2\cdot AP\cdot \sin y}=\frac{1}{2\cdot AP}$．
又 $AP=BC$，推出 $\sin3x=\frac{1}{2}$；
$4x<180$，推出 $3x=30$，所以 $x=10$．
故 $y=70$，$r=\frac{10+70}{2\cdot70}=\frac{4}{7}$．
因此求出 $1000r=571+\frac{3}{7}$．
故 $\left[ 1000r\right]=571$．
答案
解析
备注
