梯形的一条底边比另一条底边长100个单位.梯形两腰中点的连线把梯形分成面积比为 $2:3$ 的两部分.设 $x$ 是连接梯形的两腰,平行于梯形底边,并分梯形为面积相等的两部分的线段的长度,求出不超过 $\frac{{{x}^{2}}}{100}$ 的最大整数.
【难度】
【出处】
2000年第18届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
181
【解析】
设梯形较短的底长度为 $a$,则其较长的底长度为 $a+100$,中位线长为 $a+50$.由梯形面积计算公式及条件得 $\left( a+\left( a+50 \right) \right):\left( \left( a+50\right)+\left( a+100 \right) \right)=2:3$,解得 $a=75$,即梯形的两底长分别为75和175.
如图所示,延长梯形的两腰,交于一点 $A$.把长度为 $x$ 的那条线段画出后,图中有三个彼此相似的三角形,它们的面积比为 ${{75}^{2}}:{{x}^{2}}:{{175}^{2}}$,且由条件知它们的面积成等差数列.因此 ${{x}^{2}}=\frac{{{75}^{2}}+{{175}^{2}}}{2}=18125$,故所求为 $181$.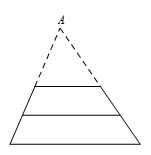
如图所示,延长梯形的两腰,交于一点 $A$.把长度为 $x$ 的那条线段画出后,图中有三个彼此相似的三角形,它们的面积比为 ${{75}^{2}}:{{x}^{2}}:{{175}^{2}}$,且由条件知它们的面积成等差数列.因此 ${{x}^{2}}=\frac{{{75}^{2}}+{{175}^{2}}}{2}=18125$,故所求为 $181$.

答案
解析
备注