如图所示，点 $A$，$B$，$C$ 在以点 $O$ 为球心，20为半径的球面上．已知 $AB=13$，$BC=14$，$CA=15$，点 $O$ 到三角形 $ABC$ 所在平面的距离为 $\frac{m\sqrt{n}}{k}$，其中 $m$，$n$，$k$ 是正整数，$m$ 与 $k$ 互素，$n$ 不能被任何素数的平方整除．求 $m+n+k$．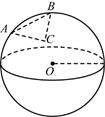
【难度】
【出处】
2000年第18届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
118
【解析】
如图所示，设点 $O$ 到三角形 $ABC$ 所在平面的垂足为 $K$．由勾股定理得
$A{{K}^{2}}=O{{A}^{2}}-O{{K}^{2}}$，$B{{K}^{2}}=O{{B}^{2}}-O{{K}^{2}}$，$C{{K}^{2}}=O{{C}^{2}}-O{{K}^{2}}$．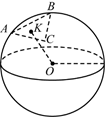
由 $OA=OB=OC$ 得 $AK=BK=CK$，故 $K$ 是 $\vartriangle ABC$ 的外心．
由余弦定理得 $\cos \angle BAC=\frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2AB\cdot AC}=\frac{198}{390}=\frac{33}{65}$．
因此 $\sin \angle BAC=\sqrt{1-{{\left( \frac{33}{65} \right)}^{2}}}=\frac{56}{65}$．
故 $AK=\frac{BC}{2\sin\angle BAC}=\frac{14}{2\cdot \frac{56}{65}}=\frac{65}{8}$．
因此 $OK=\sqrt{O{{A}^{2}}-A{{K}^{2}}}=\sqrt{{{20}^{2}}-{{\left(\frac{65}{8} \right)}^{2}}}=\frac{15\sqrt{95}}{8}$．
故 $m=15$，$n=95$，$k=8$，从而 $m+n+k=118$．
$A{{K}^{2}}=O{{A}^{2}}-O{{K}^{2}}$，$B{{K}^{2}}=O{{B}^{2}}-O{{K}^{2}}$，$C{{K}^{2}}=O{{C}^{2}}-O{{K}^{2}}$．
由 $OA=OB=OC$ 得 $AK=BK=CK$，故 $K$ 是 $\vartriangle ABC$ 的外心．由余弦定理得 $\cos \angle BAC=\frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2AB\cdot AC}=\frac{198}{390}=\frac{33}{65}$．
因此 $\sin \angle BAC=\sqrt{1-{{\left( \frac{33}{65} \right)}^{2}}}=\frac{56}{65}$．
故 $AK=\frac{BC}{2\sin\angle BAC}=\frac{14}{2\cdot \frac{56}{65}}=\frac{65}{8}$．
因此 $OK=\sqrt{O{{A}^{2}}-A{{K}^{2}}}=\sqrt{{{20}^{2}}-{{\left(\frac{65}{8} \right)}^{2}}}=\frac{15\sqrt{95}}{8}$．
故 $m=15$，$n=95$，$k=8$，从而 $m+n+k=118$．
答案
解析
备注
