在 $\vartriangle ABC$ 中,$\angle A=60{}^\circ $,$\angle B=45{}^\circ $.$\angle A$ 的角平分线交 $BC$ 于点 $T$,且 $AT=24$.$\vartriangle ABC$ 的面积可以写成 $a+b\sqrt{c}$,其中 $a$,$b$,$c$ 都是正整数,且 $c$ 不能被任何素数的平方整除.求 $a+b+c$.
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
291
【解析】
如图所示,注意到 $\angle C$ 与 $\angle ATC$ 都是 $75{}^\circ $,因此 $AC=AT=24$.作 $\vartriangle ABC$ 的高 $CD$.易知 $\vartriangle ADC$ 的各角分别为 $30{}^\circ -60{}^\circ -90{}^\circ $,$\vartriangle BDC$ 的各角分别为 $45{}^\circ-45{}^\circ -90{}^\circ $.因此 $AD=12$,$BD=CD=12\sqrt{3}$.故三角形 $ABC$ 的面积为 $\frac{12\sqrt{3}\left( 12+12\sqrt{3} \right)}{2}=216+72\sqrt{3}$.
因此 $a+b+c=291$.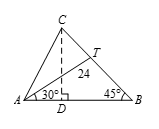
因此 $a+b+c=291$.

答案
解析
备注