设 $ABCD$ 是圆内接正方形,正方形 $EFGH$ 的顶点 $E$ 和 $F$ 在边 $CD$ 上,顶点 $G$ 和 $H$ 在圆上.若 $\frac{{{S}_{EFGH}}}{{{S}_{ABCD}}}=\frac{m}{n}$,其中 $m$,$n$ 是互素的正整数且 $m<n$.求 $10n+m$.
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
251
【解析】
如图所示,设 $O$ 为圆心,分别用 $x$,$s$ 代表小正方形和大正方形的边长.作 $OL$ 垂直 $BC$ 于 $L$,作 $FK$ 垂直 $OL$ 于 $K$.故 $GK=GF+FK=GF+GL=x+\frac{s}{2}$,$OK=\frac{x}{2}$,且圆的半径为 $\frac{1}{2}s\sqrt{2}$.应用勾股定理得 ${{\left(x+\frac{s}{2} \right)}^{2}}+{{\left( \frac{x}{2} \right)}^{2}}={{\left(\frac{s\sqrt{2}}{2} \right)}^{2}}$.展开得 ${{x}^{2}}+sx+\frac{{{s}^{2}}}{4}+\frac{{{x}^{2}}}{4}=\frac{{{s}^{2}}}{2}$,故 $5{{x}^{2}}+4sx-{{s}^{2}}=0$,即 $\left(5x-s \right)\left( x+s \right)=0$,因此 $x=\frac{s}{5}$.两个正方形的面积比是 $\frac{1}{25}$,因此 $10n+m=251$.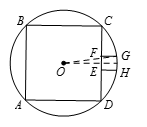

答案
解析
备注