设 $\vartriangle PQR$ 为直角三角形,其中 $PQ=90$,$PR=120$,$QR=150$.记 $\vartriangle PQR$ 的内切圆为 ${{C}_{1}}$.直线 $ST$ 垂直于 $PR$ 且与圆 ${{C}_{1}}$ 相切,分别交 $PR$ 与 $QR$ 于点 $S$ 及 $T$.又作直线 $UV$ 垂直于 $PQ$ 且与圆 ${{C}_{1}}$ 相切,分别交 $PQ$ 及 $QR$ 于点 $U$ 及 $V$.记 $\vartriangle RST$ 的内切圆为 ${{C}_{2}}$,$\vartriangle QUV$ 的内切圆为 ${{C}_{3}}$.若圆 ${{C}_{2}}$ 与 ${{C}_{3}}$ 的圆心距可以表示为 $\sqrt{10n}$,求 $n$.
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
725
【解析】
如图所示,设 ${{C}_{1}}$,${{C}_{2}}$,${{C}_{3}}$ 的半径分别为 ${{r}_{1}}$,${{r}_{2}}$,${{r}_{3}}$,任意三角形的内径为面积的两倍除以周长,故 ${{r}_{1}}=90\cdot \frac{120}{\left( 90+120+150 \right)}=30$.由于 $\vartriangle RST$ 与 $\vartriangle RPQ$ 相似,且 $RS=PR-2{{R}_{1}}=60$,二者的相似比是 $1:2$,故 ${{r}_{2}}=15$.同理可得 ${{r}_{3}}=10$.设 $d$ 为圆 ${{C}_{2}}$,${{C}_{3}}$ 的圆心距离,则
${{d}^{2}}={{\left(2{{r}_{1}}+{{r}_{2}}-{{r}_{3}} \right)}^{2}}+{{\left(2{{r}_{1}}+{{r}_{3}}-{{r}_{2}} \right)}^{2}}$
$={{65}^{2}}+{{55}^{2}}=4225+3025=7250$.
因此,$n=725$.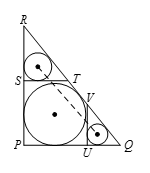
${{d}^{2}}={{\left(2{{r}_{1}}+{{r}_{2}}-{{r}_{3}} \right)}^{2}}+{{\left(2{{r}_{1}}+{{r}_{3}}-{{r}_{2}} \right)}^{2}}$
$={{65}^{2}}+{{55}^{2}}=4225+3025=7250$.
因此,$n=725$.

答案
解析
备注