查看数据源：5c78f23e210b28428f14cfd2
将一 $3\times 3$ 单位正方形的每个方格等概率随机地染成蓝色或红色．若在此 $3\times 3$ 单位正方形中没有任何一个 $2\times 2$ 的单位正方形所包含的四个方格都是红色的概率为 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数．求 $m+n$．
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
  • 题型
    >
    计数与概率
    >
    概率计算题
  • 知识点
    >
    计数与概率
    >
    计数中的常用知识
    >
    容斥原理
【答案】
929
【解析】
如图所示，给这些方格上数字，对 $i=1 ,2 ,4 ,5$，设 ${{\theta }_{i}}$ 为以 $i$ 为左上角的 $2\times2$ 方格染红．设 $P\left( E \right)$ 为性质 $E$ 出现的概率．由容斥原理，图中至少出现一个 $2\times 2$ 全红方格的概率为
$P\left({{Q}_{1}} \right)+P\left( {{Q}_{2}} \right)+P\left( {{Q}_{3}} \right)+P\left({{Q}_{4}} \right)$ $-P\left( {{Q}_{1}}\bigcap {{Q}_{2}} \right)-P\left({{Q}_{1}}\bigcap {{Q}_{4}} \right)-P\left( {{Q}_{2}}\bigcap {{Q}_{5}}\right)-P\left( {{Q}_{4}}\bigcap {{Q}_{5}} \right)-P\left( {{Q}_{1}}\bigcap{{Q}_{5}} \right)$
$-P\left({{Q}_{2}}\bigcap {{Q}_{4}} \right)+P\left( {{Q}_{1}}\bigcap {{Q}_{2}}\bigcap{{Q}_{5}} \right)+P\left( {{Q}_{1}}\bigcap {{Q}_{2}}\bigcap {{Q}_{4}}\right)+P\left( {{Q}_{1}}\bigcap {{Q}_{4}}\bigcap {{Q}_{5}} \right)$
$+P\left({{Q}_{2}}\bigcap {{Q}_{4}}\bigcap {{Q}_{5}} \right)-P\left( {{Q}_{1}}\bigcap{{Q}_{2}}\bigcap {{Q}_{4}}\bigcap {{Q}_{5}} \right)$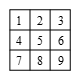，即 $4{{\left(\frac{1}{2} \right)}^{4}}-4\left[ 4{{\left( \frac{1}{2} \right)}^{6}}+2{{\left(\frac{1}{2} \right)}^{7}} \right]+4{{\left( \frac{1}{2} \right)}^{8}}-{{\left(\frac{1}{2} \right)}^{9}}=\frac{95}{512}$．
因此，不存在 $2\times 2$ 全红方格的概率为 $1-\frac{95}{512}=\frac{417}{512}$，故 $m+n=929$．
答案 解析 备注
0.121615s