连接一三角形三边中点所得到的三角形,称为该三角形的中点三角形.现定义一序列多面体 ${{P}_{i}}$ 如下:设 ${{P}_{0}}$ 表示为体积为1的正四面体,${{P}_{i}}$ 及以其每一个面上的中点三角形为一面再向外作正四面体所构成的新多面体图形为 ${{P}_{i+1}}$.若 ${{P}_{3}}$ 的体积为 $\frac{m}{n}$,其中 $m$,$n$ 是互素的正整数.求 $m+n$.
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
101
【解析】
图中画出了 ${{P}_{1}}$,注意 ${{P}_{0}}$ 有4个面,${{P}_{1}}$ 有24个面,由归纳法易知 ${{P}_{i}}$ 有 $4\cdot{{6}^{i}}$ 个面,这个数也是 ${{P}_{i}}$ 到 ${{P}_{i+1}}$ 时增加的小四面体的个数.每个小四面体体积为 ${{\left( \frac{1}{8} \right)}^{i+1}}$,故 ${{P}_{i+1}}$ 比 ${{P}_{i}}$ 的体积大 $4\cdot{{6}^{i}}{{\left( \frac{1}{8} \right)}^{i+1}}=\left( \frac{1}{2}\right){{\left( \frac{3}{4} \right)}^{i}}$.特别地,${{P}_{3}}$ 的体积是 $1+\left(\frac{1}{2} \right)+\left( \frac{1}{2} \right)\left( \frac{3}{4} \right)+\left(\frac{1}{2} \right){{\left( \frac{3}{4} \right)}^{2}}=\frac{69}{32}$,因此 $m+n=101$.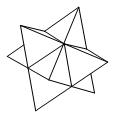

答案
解析
备注