在四边形 $ABCD$ 中,$\angle BAD=\angle ADC$,$\angle ABD=\angle BCD$,$AB=8$,$BD=10$,$BC=6$.若线段 $CD$ 的长可以表示为 $\frac{m}{n}$,其中 $m$,$n$ 是互素的正整数.求 $m+n$.
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
69
【解析】
如图所示,延长 $AB$ 与 $DC$ 交于点 $P$.由于 $\angle PCB$ 与 $\angle PBD$ 分别是 $\angle BCD$ 与 $\angle ABD$ 的补角,故它们相等.因此 $\vartriangle PCB$ 与 $\vartriangle PBD$ 相似,故 $\frac{PD-8}{PD}=\frac{PB}{PD}=\frac{CB}{BD}=\frac{6}{10}$,
因此,$PA=PD=20$,$PB=12$,$\frac{PC}{12}=\frac{6}{10}$,得 $PC=7.2$.因此 $CD=12.8=\frac{64}{5}$,故 $m+n=69$.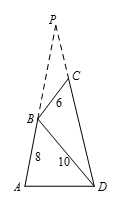
因此,$PA=PD=20$,$PB=12$,$\frac{PC}{12}=\frac{6}{10}$,得 $PC=7.2$.因此 $CD=12.8=\frac{64}{5}$,故 $m+n=69$.

答案
解析
备注