设 $EFGH$,$EFDC$ 和 $EHBC$ 为正方体的三个相邻的正方形面,其中 $EC=EI=EJ=EK=2$.现从此正方体钻出一个包含边 $IJ$,$JK$ 及 $KI$,且壁面平行于 $AE$ 的通道,设正方体去掉通道后剩余的部分为 $S$.设 $S$ 连同通道的壁面在内的表面积为 $m+n\sqrt{p}$,其中 $m$,$n$,$p$ 都是正整数,且 $p$ 不能被任何素数的平方所整除,求 $m+n+p$.
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
417
【解析】
如图所示,设各点坐标为 $A=\left( 0 ,0 ,0 \right)$,$B=\left( 8, 0, 0 \right)$,$C=\left( 8, 8 ,0 \right)$,$D=\left( 0 ,8, 0 \right)$,$I=\left( 6, 8 ,8 \right)$,$J=\left( 8, 6, 8 \right)$ 和 $k=\left( 8 ,8 ,6 \right)$.经过 $I$ 且平行于 $AE$ 的直线可以写为 $\left(x, y, z \right)=\left( 6-t ,8-t, 8-t \right)$.故当 $x=0$ 时,它与正方体再次相交于点 $L=\left(0 ,2, 2 \right)$.由于对称性,过 $J$,$K$ 与 $AE$ 平行的直线分别与正方体交于点 $M=\left( 2, 0 ,2 \right)$ 与 $N=\left( 2, 2, 0 \right)$.易知过 $I$,$J$,$L$ 的平面方程为 $2z=2+x+y$,据此平面与 $z$ 轴交于点 $O=\left( 0 ,0 ,1 \right)$.同理,这条坑道与 $x$ 轴交 $Q=\left(1 ,0 ,0 \right)$ 与 $y$ 轴交于 $P=\left( 0, 1, 0 \right)$.如图所示,坑道的一头为三角形 $IJK$,另一头为空间六边形 $LOMQNP$.$S$ 的表面包含9个多边形,三种样式,每种三个,易知五边形 $IFGHJ$ 与六边形 $CDPNQB$ 的面积均为 ${{8}^{2}}-2$.为了求出五边形 $ILOMJ$ 的面积,首先注意到 $IJ=2\sqrt{2}$,$IL=JM=6\sqrt{3}$,$LO=OM=\sqrt{5}$,故矩形 $ILMJ$ 面积是 $12\sqrt{6}$,剩下三角形 $LOM$ 面积为 $\sqrt{6}$,总面积为 $3\left( 62+62+13\sqrt{6} \right)=372+39\sqrt{6}$,故 $m+n+p=417$.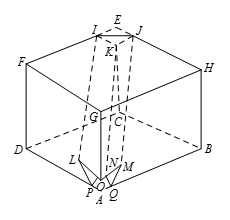

答案
解析
备注