如图所示,在一个封闭的长方形中,有20个等圆排列成三行,相邻的圆相切,且第一行和第三行的圆与长方形的长和宽相切.设长方形的长、宽之比为 $\frac{1}{2}\left( \sqrt{p-q} \right)$,其中 $p, q\in {{\mathbf{Z}}^{+}}$.求 $p+q$ 的值.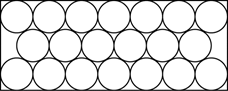

【难度】
【出处】
2002年第20届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
154
【解析】
设 $r$ 为每个小圆的半径,$l$,$w$ 分别是长方形的长和宽,且 $l>w$,由题知 $14r=l$.考虑这样一个等边三角形,它的顶点是三个彼此相切的圆的圆心,这样一个等边三角形的高为 $r\sqrt{3}$,因此 $w=2r+2r\sqrt{3}$,由此推出 $\frac{l}{w}=\frac{14r}{2r\left( 1+\sqrt{3} \right)}=\frac{7\left(\sqrt{3}-1 \right)}{2}=\frac{\sqrt{147}-7}{2}$.
因此 $p+q=154$.
因此 $p+q=154$.
答案
解析
备注