如图所示,在直角三角形 $ABC$ 中,点 $D$ 在 $BC$ 边上,线段 $AD$ 平分 $\angle CAB$,点 $E$ 和点 $F$ 分别在 $AB$ 边和 $AC$ 边上,且 $AE=3$,$AF=10$.给定 $EB=9$,$FC=27$,求最接近四边形 $DCFG$ 面积的整数.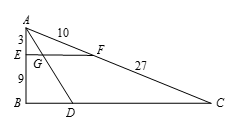

【难度】
【出处】
2002年第20届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
148
【解析】
由角平分线定理,$BD:DC=AB:AC=12:37$,因此 $\vartriangle ADC$ 的面积等于 $\vartriangle ABC$ 的 $\frac{37}{49}$;由角平分线定理,$EG:GF=AE:AF=3:10$,因此 $\vartriangle AGF$ 的面积只等于 $\vartriangle AEF$ 的 $\frac{10}{13}$.$\vartriangle AGF$ 的面积是 $\vartriangle AFB$ 的 $\frac{3}{12}$,而 $\vartriangle AFB$ 的面积等于 $\vartriangle ABC$ 的 $\frac{10}{37}$.因为 $BC=\sqrt{{{37}^{2}}-{{12}^{2}}}=35$,因此 $\vartriangle ABC$ 的面积等于210.推出四边形 $DCFG$ 面积等于
$\left(\frac{37}{49}-\frac{10}{13}\cdot \frac{3}{12}\cdot \frac{10}{37}\right)210=\frac{1110}{7}-\frac{5250}{481}=158\frac{4}{7}-10\frac{440}{481}$,
因此所求的数为148.
$\left(\frac{37}{49}-\frac{10}{13}\cdot \frac{3}{12}\cdot \frac{10}{37}\right)210=\frac{1110}{7}-\frac{5250}{481}=158\frac{4}{7}-10\frac{440}{481}$,
因此所求的数为148.
答案
解析
备注