如图所示,$\vartriangle ABC$ 中线 $AD$,$CE$ 的长分别为18,27,$AB=24$.延长 $CE$ 交 $\vartriangle ABC$ 的外接圆于点 $F$.$\vartriangle ABF$ 的面积等于 $m\sqrt{n}$,其中 $m$,$n$ 均为正整数,$n$ 不能被任何素数的平方整除.求 $m+n$ 的值.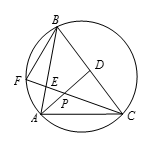

【难度】
【出处】
2002年第20届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
63
【解析】
设点 $P$ 为 $AD$ 和 $CE$ 的交点,由相交弦定理得 $\frac{EF}{12}=\frac{12}{27}$,故 $EF=\frac{16}{3}$.$\vartriangle AFB$ 的面积是 $\vartriangle AEF$ 的两倍,故 $\vartriangle AEF$ 和 $\vartriangle AEP$ 的面积之比为 $\frac{\frac{16}{3}}{9}$,这是因为三角形的中线将彼此三等分.注意到 $AE=AP=12$,即 $\vartriangle AEP$ 是等腰三角形,因此 $PE$ 边上的高为
$\sqrt{{{12}^{2}}-{{\left(\frac{9}{2}\right)}^{2}}}=\frac{1}{2}\sqrt{{{24}^{2}}-{{9}^{2}}}=\frac{3}{2}\sqrt{{{8}^{2}}-{{3}^{2}}}=\frac{3}{2}\sqrt{55}$,$\vartriangle AEP$ 的面积等于 $\left( \frac{27}{4} \right)\sqrt{55}$,因此
$\left[ AFB \right]=2\left[ AFE \right]=2\left( \frac{16}{27}\right)\cdot \left[ AEP \right]$
$=2\left(\frac{16}{27} \right)\cdot \left( \frac{27}{4} \right)\sqrt{55}=8\sqrt{55}$.
所以 $m+n=63$.
$\sqrt{{{12}^{2}}-{{\left(\frac{9}{2}\right)}^{2}}}=\frac{1}{2}\sqrt{{{24}^{2}}-{{9}^{2}}}=\frac{3}{2}\sqrt{{{8}^{2}}-{{3}^{2}}}=\frac{3}{2}\sqrt{55}$,$\vartriangle AEP$ 的面积等于 $\left( \frac{27}{4} \right)\sqrt{55}$,因此
$\left[ AFB \right]=2\left[ AFE \right]=2\left( \frac{16}{27}\right)\cdot \left[ AEP \right]$
$=2\left(\frac{16}{27} \right)\cdot \left( \frac{27}{4} \right)\sqrt{55}=8\sqrt{55}$.
所以 $m+n=63$.
答案
解析
备注