一正方体上三个顶点分别为 $P=\left( 7 ,12 ,10 \right)$,$Q=\left( 8 ,8 ,1 \right)$,$R=\left( 11, 3, 9 \right)$.试求这个正方体的表面积.
【难度】
【出处】
2002年第20届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
294
【解析】
如图所示,注意到 $\vartriangle PQR$ 是等边三角形,因为 $PQ=QR=RP=7\sqrt{2}$.由此可推出正方体的棱长等于7单位长,因此正方体的表面积 $6\left({{7}^{2}} \right)=294$.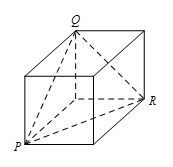

答案
解析
备注