在庭院中建造花园时，通常在花园周围的边界上铺上 $n$ 块1单位的正六边形砖块，边连着边铺出花园的轮廓．如图是当 $n=5$ 时，花园周围的砖块走道示意图．
当 $n=202$，砖块走道围成的花园面积（不包含走道面积）为 $m\left( \frac{\sqrt{3}}{2} \right)$ 平方单位，其中 $m$ 为正整数，试求 $m$ 被1000整除的余数．
当 $n=202$，砖块走道围成的花园面积（不包含走道面积）为 $m\left( \frac{\sqrt{3}}{2} \right)$ 平方单位，其中 $m$ 为正整数，试求 $m$ 被1000整除的余数．
【难度】
【出处】
2002年第20届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
803
【解析】
花园面积被正六边形砖块平均分成与砖块数相同的若干块，花园边界上的正六边形砖块从图上来看像一条小路，每边上有 $n-1$ 块砖．
如图是当 $n=10$ 时花园的面积（不包括最外围的走道）．注意到，任何 $n>1$，从左起的第一列砖块数开始数，每一列都比左边一列的砖块数多1块，直到中间那块．因为最左边一列共有 $n-1$ 块砖，最长的一列是它右边的第 $n-2$ 列，最长的一列共有 $\left( n-1 \right)+\left( n-2 \right)=2n-3$ 块正六边形砖块．花园中线的左边共有正六边形砖块：
$\left( n-1 \right)+n+\left( n+1\right)+\left( n+2 \right)+\cdots +\left[ \left( n-1 \right)+\left( n-3 \right)\right]=\frac{\left( 3n-5 \right)\left( n-2 \right)}{2}$．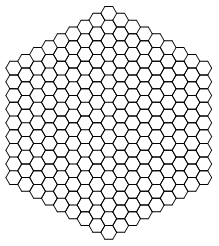
在花园右边的砖块数也相同．因为每个小正六边形的边长为1，每个小正六边形有六个小正三角形，那么花园的面积等于 $\left[ \left( 2n-3\right)+\left( 3n-5 \right)\left( n-2 \right) \right]\left[ \frac{6\sqrt{3}}{4}\right]$．
当 $n=202$ 时，面积为 $\frac{361803\sqrt{3}}{2}$ 个单位面积，因此所求的余数等于803．
如图是当 $n=10$ 时花园的面积（不包括最外围的走道）．注意到，任何 $n>1$，从左起的第一列砖块数开始数，每一列都比左边一列的砖块数多1块，直到中间那块．因为最左边一列共有 $n-1$ 块砖，最长的一列是它右边的第 $n-2$ 列，最长的一列共有 $\left( n-1 \right)+\left( n-2 \right)=2n-3$ 块正六边形砖块．花园中线的左边共有正六边形砖块：
$\left( n-1 \right)+n+\left( n+1\right)+\left( n+2 \right)+\cdots +\left[ \left( n-1 \right)+\left( n-3 \right)\right]=\frac{\left( 3n-5 \right)\left( n-2 \right)}{2}$．
在花园右边的砖块数也相同．因为每个小正六边形的边长为1，每个小正六边形有六个小正三角形，那么花园的面积等于 $\left[ \left( 2n-3\right)+\left( 3n-5 \right)\left( n-2 \right) \right]\left[ \frac{6\sqrt{3}}{4}\right]$．当 $n=202$ 时，面积为 $\frac{361803\sqrt{3}}{2}$ 个单位面积，因此所求的余数等于803．
答案
解析
备注
