一个篮球选手每次投篮的命中率均为一个常数 $0.4$，与之前的投篮无关．设 ${{a}_{n}}$ 为 $n$ 次投篮后的命中率（进球数与 $n$ 的比值），则出现 ${{a}_{10}}=0.4$，且对于 $1\leqslant n\leqslant 9$，${{a}_{n}}\leqslant 0.4$ 的概率可表示为 $\frac{{{p}^{a}}{{q}^{b}}r}{{{s}^{c}}}$，$p$，$q$ $r$，$s$ 为素数，$a$，$b$，$c$ 为正整数．试求 $\left( p+q+r+s \right)\left( a+b+c \right)$ 的值．
【难度】
【出处】
2002年第20届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
660
【解析】
设 $x$ 为篮球选手投球次数，$y$ 为篮球选手投中次数．当 $x=1 2 \cdots 10 y$ 的最大值分别为 $ 0,0,1,1,2,2,2,3,3,4$．因为 $x=10$，$y=4$，当 $x=$ $ 9,8,7,6,5,4,3,2,1$，$y$ 的最大值分别为 $ 3,2,1,0,0,0,0,0,0$．我们将可能的投中和投球情况的数列表示在图中．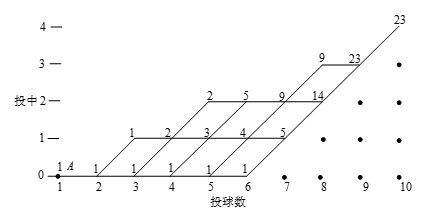
可能的投中和投球情况的数列与有序数对 $\left(x y \right)$ 一致，其中 $x$ 为篮球选手投球次数，$y$ 为篮球选手投中次数，开始是 $\left( 1 0 \right)$，最后是 $\left( 10 4\right)$．每一种顺序与下图中每一条从 $A\to B$ 的路径一致，向右或向上移动．在图中，从 $A$ 到任意一点 $P$ 的方法数等于从 $A$ 到达 $P$ 点之前的方法数之和．图中每一点上都标记了从 $A$ 到该点所有可能的方法数．因此 $A\to B$ 的方法数是23．每条路径代表了4次投中和6次没有投中的顺序，因此所求的概率是
$23\cdot{{\left( 0.4 \right)}^{4}}{{\left( 0.6\right)}^{6}}=\frac{{{2}^{4}}{{3}^{6}}23}{{{5}^{10}}}$．
那么 $\left( p+q+r+s\right)\left( a+b+c \right)=\left( 2+3+23+5 \right)\left( 4+6+10 \right)=660$．
可能的投中和投球情况的数列与有序数对 $\left(x y \right)$ 一致，其中 $x$ 为篮球选手投球次数，$y$ 为篮球选手投中次数，开始是 $\left( 1 0 \right)$，最后是 $\left( 10 4\right)$．每一种顺序与下图中每一条从 $A\to B$ 的路径一致，向右或向上移动．在图中，从 $A$ 到任意一点 $P$ 的方法数等于从 $A$ 到达 $P$ 点之前的方法数之和．图中每一点上都标记了从 $A$ 到该点所有可能的方法数．因此 $A\to B$ 的方法数是23．每条路径代表了4次投中和6次没有投中的顺序，因此所求的概率是$23\cdot{{\left( 0.4 \right)}^{4}}{{\left( 0.6\right)}^{6}}=\frac{{{2}^{4}}{{3}^{6}}23}{{{5}^{10}}}$．
那么 $\left( p+q+r+s\right)\left( a+b+c \right)=\left( 2+3+23+5 \right)\left( 4+6+10 \right)=660$．
答案
解析
备注
