在凸四边形 $ABCD$ 中,$\angle A=\angle C$,$AB=CD=180$,$AD\ne BC$,若四边形周长为640,求 $\left[ 1000\cos A \right]$($\left[ x \right]$ 表示不超过 $x$ 的最大整数).
【难度】
【出处】
2003年第21届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
777
【解析】
如图21-2所示,令 $\angle A=\angle C=\alpha $,$AD=x$,$BC=y$.在 $\vartriangle ABD$ 和 $\vartriangle CBD$ 中由余弦定理得
$B{{D}^{2}}={{x}^{2}}+{{180}^{2}}-2\cdot x\cos \alpha $
$={{y}^{2}}+{{180}^{2}}-2\cdot 180y\cos \alpha $.
由于 $x\ne y$,故 $\cos \alpha=\frac{{{x}^{2}}-{{y}^{2}}}{2\times 180\left( x-y\right)}=\frac{x+y}{360}=\frac{7}{9}$,因此 $\left[ 1000\cos A\right]=777$.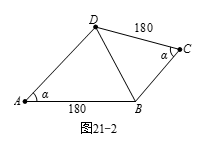
$B{{D}^{2}}={{x}^{2}}+{{180}^{2}}-2\cdot x\cos \alpha $
$={{y}^{2}}+{{180}^{2}}-2\cdot 180y\cos \alpha $.
由于 $x\ne y$,故 $\cos \alpha=\frac{{{x}^{2}}-{{y}^{2}}}{2\times 180\left( x-y\right)}=\frac{x+y}{360}=\frac{7}{9}$,因此 $\left[ 1000\cos A\right]=777$.

答案
解析
备注