如图22-3所示,将一张长方形纸 $ABCD$ 中顶点为 $B$ 的一角折起来,使得顶点 $B$ 与 $AD$ 边上的点 ${B}'$ 重合。设折痕为 $EF$,其中 $E$ 点在 $AB$ 边上,$F$ 点在 $CD$ 边上.已知:$AE=8$,$BE=17$,$CF=3$,长方形 $ABCD$ 的周长为 $\frac{m}{n}$,其中 $m n$ 为互素的正整数,试求 $m+n$ 的值。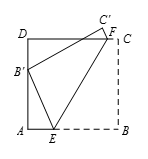

【难度】
【出处】
2004年第22届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
293
【解析】
首先注意到 ${B}'{E}'=BE=17$,在 $\vartriangle EA{B}'$ 中由勾股定理可得 $A{B}'=15$ 。作 $FG\parallel CB$ 交边 $AB$ 于点 $G$,显然有 $GE=17-3=14$ 。
由于点 $B$ 沿着 $EF$ 折叠得到点 ${B}'$,故 $EF\bot B{B}'$,因此 $\vartriangle EGF\sim\vartriangle {B}'AB$,故 $\frac{FG}{BA}=\frac{GE}{AB}$,解得 $FG=\frac{70}{3}$ 。
因此长方形 $ABCD$ 的周长为 $\left( \frac{70}{3}+25\right)\times 2=\frac{290}{3}$,即 $m+n=293$ 。
由于点 $B$ 沿着 $EF$ 折叠得到点 ${B}'$,故 $EF\bot B{B}'$,因此 $\vartriangle EGF\sim\vartriangle {B}'AB$,故 $\frac{FG}{BA}=\frac{GE}{AB}$,解得 $FG=\frac{70}{3}$ 。
因此长方形 $ABCD$ 的周长为 $\left( \frac{70}{3}+25\right)\times 2=\frac{290}{3}$,即 $m+n=293$ 。
答案
解析
备注