设 $ABCD$ 为等腰梯形,$AB=6 BC=DA=5 CD=4$ 。分别以 $A$ 和 $B$ 为圆心,$3$ 为半径各画一个圆;再以 $C$ 和 $D$ 为圆心,$2$ 为半径各画一个圆。在梯形内部有一个圆,它与上述的四个圆都相切。此圆的半径为 $\frac{-k+m\sqrt{n}}{p}$,其中 $k m n p$ 均为正整数,$n$ 不能被任何素数的平方整除,$k$ 和 $p$ 互素。试求 $k+m+n+p$ 的值。
【难度】
【出处】
2004年第22届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
134
【解析】
如图 $22-4$ 所示,设 $E$ 是 $AB$ 的中点,$F$ 是 $CD$ 的中点,$x$ 为该圆的半径,$G$ 为该圆的圆心,那么 $GE\bot AB$,$AG=x+3$ 。在 $\vartriangle AEG$ 中由勾股定理可得 $GE=\sqrt{{{x}^{2}}+6x}$,同理可得 $FG=\sqrt{{{x}^{2}}+4x}$ 。因为这个梯形的高为 $\sqrt{{{5}^{2}}-{{\left(\frac{6-4}{2} \right)}^{2}}}=\sqrt{24}$,故 $\sqrt{{{x}^{2}}+6x}+\sqrt{{{x}^{2}}+4x}=\sqrt{24}$,因此 $\sqrt{{{x}^{2}}+6x}=\sqrt{24}-\sqrt{{{x}^{2}}+4x}$,两边平方得 ${{x}^{2}}+6x=24+{{x}^{2}}+4x-2\sqrt{24\left({{x}^{2}}+4x \right)}$ 。化简得 $\sqrt{24+\left( {{x}^{2}}+4x \right)}=12-x$,两边再平方并整理的 $23{{x}^{2}}+120x-144=0$,故 $x=\frac{-60+48\sqrt{3}}{23}$(舍去负根)。因此 $k+m+n+p=60+48+3+23=134$ 。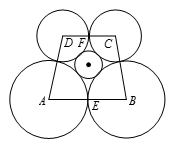

答案
解析
备注