有27个单位正方体,每个正方体有4个面涂成金黄色,且没有涂色的两个面有公共棱。这27个单位正方体随机组成一个 $3\times 3\times 3$ 的大正方体,假设大正方体的6个面都是黄色的概率为 $\frac{{{p}^{\circ }}}{{{q}^{b}}{{r}^{c}}}$,其中 $p$,$q$,$r$ 是不同的素数,$a$,$b$,$c$ 是正整数,求 $p+q+r+a+b+c$ 。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
74
【解析】
组成大正方体的27个单位正方体中,有6个只有一个面显露在大正方体的表面,12个有两个面显露在大主方体的表面,8个有三个面显露在大正方体的表面。
因为没涂色的两个面有公共棱,所以只要其中一个面出现在大正方体表面,则公共棱一定也会出现在大正方体的表面。因此我们只要计算出公共棱不出现在大正方体的表面的概率即可。
如图23-4所示,一个正方体有12条棱,位于大正方体顶点的单位正方体(如单位正方体 $C$),棱上的单位正方体(如单位正方体 $B$),面中间的单位正方体(如单位正方体 $A$)分别有9,7,4条棱显露在大正方体的表面上。
所以大正方体6个面都是黄色的概率为
${{\left( \frac{12-9}{12} \right)}^{8}}\cdot {{\left(\frac{12-7}{12} \right)}^{12}}\cdot {{\left( \frac{12-4}{12}\right)}^{6}}=\frac{{{5}_{12}}}{{{2}^{34}}\cdot {{3}^{18}}}$
从而 $a=12$,$b=34$,$c=18$,$p=5$,$b=2$,$c=3$,所以 $p+q+r+a+b+c=74$ 。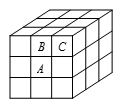
因为没涂色的两个面有公共棱,所以只要其中一个面出现在大正方体表面,则公共棱一定也会出现在大正方体的表面。因此我们只要计算出公共棱不出现在大正方体的表面的概率即可。
如图23-4所示,一个正方体有12条棱,位于大正方体顶点的单位正方体(如单位正方体 $C$),棱上的单位正方体(如单位正方体 $B$),面中间的单位正方体(如单位正方体 $A$)分别有9,7,4条棱显露在大正方体的表面上。
所以大正方体6个面都是黄色的概率为
${{\left( \frac{12-9}{12} \right)}^{8}}\cdot {{\left(\frac{12-7}{12} \right)}^{12}}\cdot {{\left( \frac{12-4}{12}\right)}^{6}}=\frac{{{5}_{12}}}{{{2}^{34}}\cdot {{3}^{18}}}$
从而 $a=12$,$b=34$,$c=18$,$p=5$,$b=2$,$c=3$,所以 $p+q+r+a+b+c=74$ 。

答案
解析
备注