一个直径为 $d$ 这的半圆完全包含在边长为8的正方形内，假设 $d$ 的最大值为 $m-\sqrt{n}$，其中 $m$，$n$ 是整数，求 $m+n$ 。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
544
【解析】
如图23-6所示，为了使半圆尽量大，也就是 $d$ 取得最大值，半圆直径的两个端点必须在正方形的两条邻边上，并且半圆与正方形另外两边相切。令正方形的四个顶点为 $A$，$B$，$C$，$D$，半圆的圆心为 $O$，直径的两个端点为 ${{B}_{1}},{{C}_{1}}$，故 ${{B}_{1}},{{C}_{1}}=d$ 。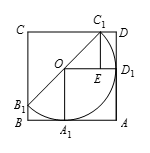
不妨设 ${{B}_{1}}$ 在边上 $BC$ 上，${{C}_{1}}$ 在边 $CD$ 上，半圆 $O$ 与边 $BA$ 相切于点 ${{A}_{1}}$，与边 $AD$ 相切于点 ${{D}_{1}}$，连 $O{{A}_{1}}$，$O{{D}_{1}}$，则 $O{{A}_{1}}=O{{D}_{1}}=\frac{d}{2}$，且 $\angle O{{A}_{1}}A=\angle O{{D}_{1}}A={{90}^{\circ }}$，所以四边形 $O{{A}_{1}}A{{D}_{1}}$ 是正方形，由此可知半圆 $O$ 关于直线 $AC$ 对称，从而 $\angle{{C}_{1}}O{{D}_{1}}={{45}^{\circ }}$ 。
过 ${{C}_{1}}$ 作 ${{C}_{1}}E\bot O{{D}_{1}}$ 于点 $E$，则乙 $\angle{{C}_{1}}E=\frac{{{C}_{1}}O}{\sqrt{2}}=\frac{d}{\sqrt{2}}$，故 $8={{C}_{1}}E+O{{A}_{1}}=\frac{d}{2\sqrt{2}}+\frac{d}{2}$，由此解出 $d=\frac{8}{\frac{1}{2\sqrt{2}}+\frac{1}{2}}=32-\sqrt{512}$，因此 $m+n=544$ 。
不妨设 ${{B}_{1}}$ 在边上 $BC$ 上，${{C}_{1}}$ 在边 $CD$ 上，半圆 $O$ 与边 $BA$ 相切于点 ${{A}_{1}}$，与边 $AD$ 相切于点 ${{D}_{1}}$，连 $O{{A}_{1}}$，$O{{D}_{1}}$，则 $O{{A}_{1}}=O{{D}_{1}}=\frac{d}{2}$，且 $\angle O{{A}_{1}}A=\angle O{{D}_{1}}A={{90}^{\circ }}$，所以四边形 $O{{A}_{1}}A{{D}_{1}}$ 是正方形，由此可知半圆 $O$ 关于直线 $AC$ 对称，从而 $\angle{{C}_{1}}O{{D}_{1}}={{45}^{\circ }}$ 。过 ${{C}_{1}}$ 作 ${{C}_{1}}E\bot O{{D}_{1}}$ 于点 $E$，则乙 $\angle{{C}_{1}}E=\frac{{{C}_{1}}O}{\sqrt{2}}=\frac{d}{\sqrt{2}}$，故 $8={{C}_{1}}E+O{{A}_{1}}=\frac{d}{2\sqrt{2}}+\frac{d}{2}$，由此解出 $d=\frac{8}{\frac{1}{2\sqrt{2}}+\frac{1}{2}}=32-\sqrt{512}$，因此 $m+n=544$ 。
答案
解析
备注
