在平面直角坐标平系中有四个点 $A\left( 0, 12 \right)$，$B\left( 10 ,9 \right)$，$C\left( 8, 0 \right)$，$C\left( 8 ,0 \right)$，$D\left( -4 ,7 \right)$，有唯一的正方形 $S$ 使得 $A$，$B$，$C$，$D$ 分别在 $S$ 的四条边上，设正方形 $S$ 的面积为 $K$，求 $10K$ 除以1000的余数。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
936
【解析】
由于连接正方形两组对边上的点的两条线段必须相交，且 $ABCD$ 是凸四边形，故 $A$ 和 $C$ 必然在正方形的一组对边上，$B$ 和 $D$ 在另一组对边上。如图所示，在平面上取一点 $E$ 使得线段 $AE$ 与 $DB$ 相交，$AE\bot DB$ 且 $AE=DB$ 。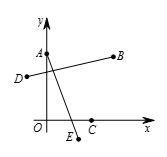
由于 $AE\bot DB$，故 $AE$ 与 $A$ 所在的边的夹角等于 $BD$ 与 $B$ 所在的边的夹角。结合 $AE=DB$ 知点 $E$ 到 $A$ 所在的边的距离等于点 $D$ 到 $B$ 所在的边的距离，即等于正方形的边长。再由线段 $AE$ 与 $DB$ 相交可知 $E$ 和 $C$ 在正方形的同一条边上。
设 $E$ 点的坐标为 $\left({{x}_{E}} {{y}_{E}} \right)$，由 $AE$ 与 $DB$ 相交，$AE\bot DB$，$AE=DB$ 得
$9-7={{x}_{E}}-0$，$10-\left(-4 \right)=12-{{y}_{E}}$ 。
因此 ${{x}_{E}}=2$，${{y}_{E}}=-2$ 。因此 $E$，$C$ 所在的边的方程为 $\frac{x-8}{y-0}=\frac{8-2}{0-\left(-1 \right)}$，即 $x-3y-8=0$ 。点 $A$ 到此边的距离为 $\frac{\left|10-3\cdot 12-8 \right|}{\sqrt{{{1}^{2}}+{{3}^{2}}}}=\frac{44}{\sqrt{10}}$，这就是正方形的边长，故 $K={{\left(\frac{44}{\sqrt{20}} \right)}^{2}}=\frac{1936}{10}$，即 $10K=1936$ 除以1000的余数为936。
由于 $AE\bot DB$，故 $AE$ 与 $A$ 所在的边的夹角等于 $BD$ 与 $B$ 所在的边的夹角。结合 $AE=DB$ 知点 $E$ 到 $A$ 所在的边的距离等于点 $D$ 到 $B$ 所在的边的距离，即等于正方形的边长。再由线段 $AE$ 与 $DB$ 相交可知 $E$ 和 $C$ 在正方形的同一条边上。设 $E$ 点的坐标为 $\left({{x}_{E}} {{y}_{E}} \right)$，由 $AE$ 与 $DB$ 相交，$AE\bot DB$，$AE=DB$ 得
$9-7={{x}_{E}}-0$，$10-\left(-4 \right)=12-{{y}_{E}}$ 。
因此 ${{x}_{E}}=2$，${{y}_{E}}=-2$ 。因此 $E$，$C$ 所在的边的方程为 $\frac{x-8}{y-0}=\frac{8-2}{0-\left(-1 \right)}$，即 $x-3y-8=0$ 。点 $A$ 到此边的距离为 $\frac{\left|10-3\cdot 12-8 \right|}{\sqrt{{{1}^{2}}+{{3}^{2}}}}=\frac{44}{\sqrt{10}}$，这就是正方形的边长，故 $K={{\left(\frac{44}{\sqrt{20}} \right)}^{2}}=\frac{1936}{10}$，即 $10K=1936$ 除以1000的余数为936。
答案
解析
备注
