如表23-1和表23-2所示,将写有1到 ${{2}_{n}}$ 编号的一叠卡片 $M$ 按顺序从上到下排列,把上面的前 $n$ 张卡片保持原来的顺序取出,组成 $A$ 堆,剩下的卡片组成 $B$ 堆。轮流从 $A$、$B$ 堆的上面各取一张并叠起来组成新的一叠卡片 $C$ 堆,在这个过程中,卡片 $n+1$ 在 $C$ 堆的最下面,卡片1在卡片 $n+1$ 的上面,以此类推,直到 $A$、$B$ 堆都取完。在重组后,、堆至少有一张卡片在 $C$ 堆的位置与它在最开始一叠卡片中的位置相同,那么称 $C$ 堆为魔术牌。例如,8张卡片可以组成一叠魔术牌,因为卡片3和卡片6在 ${C}'$ 和 ${M}'$ 堆中所处的位置相同。在一叠卡片中,卡片131在 $C$ 堆和 $M$ 堆中所处的位置相同,试求这叠卡片的数量。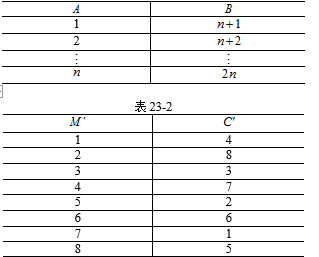

【难度】
【出处】
2005年第23届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
392
【解析】
根据重组的计算法则,可对一般情况列表进行重组。
可以从表中看出,$131$ 是第 $131$ 个数字,根据 $131$ 的位置来求 $n.A$ 堆的卡片从 $n$ 到1在 $C$ 堆中分别处于第 $1,3,5,7,\cdots$ 的位置,所以 $131$ 在 $A$ 堆中卡表中看出131是 $A$ 堆卡片从 $n$ 开始数的第 $66$ 个数,因此有 $n-65=131$,即 $n=196$,故 $2n=392$ 。
可以从表中看出,$131$ 是第 $131$ 个数字,根据 $131$ 的位置来求 $n.A$ 堆的卡片从 $n$ 到1在 $C$ 堆中分别处于第 $1,3,5,7,\cdots$ 的位置,所以 $131$ 在 $A$ 堆中卡表中看出131是 $A$ 堆卡片从 $n$ 开始数的第 $66$ 个数,因此有 $n-65=131$,即 $n=196$,故 $2n=392$ 。
答案
解析
备注