$\odot {{C}_{1}}$，$\odot {{C}_{2}}$ 相外切，并同时内切于 $\odot {{C}_{3}}$，$\odot {{C}_{1}}$，$\odot {{C}_{2}}$ 的半径分别为4，10，且三个圆的圆心共线。 $\odot {{C}_{3}}$ 内的一条弦是的 $\odot {{C}_{1}}$，公切线，设这条弦长为 $\frac{m\sqrt{n}}{p}$，其中 $m$，$n$，$p$ 是正整数，$m$ 与 $n$ 互素，$n$ 不能被任何素数的平方整除，试求 $m+n+p$ 。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
405
【解析】
如图所示，设 $A$，$B$，$F$ 分别为 $\odot{{C}_{1}}$，$\odot {{C}_{2}}$，$\odot{{C}_{3}}$ 的圆心，$P Q$ 是直线 $AB$ 与 $\odot{{C}_{3}}$ 的两个交点。 $\odot {{C}_{3}}$ 的弦 $DE$ 是 $\odot{{C}_{1}}$，${{C}_{2}}$ 的公切线，交 $\odot{{C}_{3}}$ 于点 $D$，$E$，$I$，$J$ 为切点，连接 $FD$ 。过点 $F$ 作 $FG\bot DE$，垂足为 $G$ 。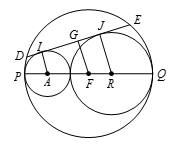
显然大圆直径等于两个小圆直径之和，故大圆的半径为 $\text{4}+\text{1}0=\text{14}$，故 $AF=14-4=10$，$BF=14-10=4$ 注意到 $AI\parallel FG\parallel BJ$，由平行线分线段成比例定理得 $\frac{FG=AI}{BJ-FG}=\frac{AF}{BF}$，将 $AI=BF=4$，$BJ=AF=10$ 代入解得 $FG=\frac{58}{7}$ 。因此
$DF=2DG=2\sqrt{D{{F}^{2}}-F{{G}^{2}}}=2\sqrt{{{14}^{2}}-{{\left(\frac{58}{7} \right)}^{2}}}=\frac{8\sqrt{390}}{7}$ 。
故 $m+n+p=8+390+7=405$ 。
显然大圆直径等于两个小圆直径之和，故大圆的半径为 $\text{4}+\text{1}0=\text{14}$，故 $AF=14-4=10$，$BF=14-10=4$ 注意到 $AI\parallel FG\parallel BJ$，由平行线分线段成比例定理得 $\frac{FG=AI}{BJ-FG}=\frac{AF}{BF}$，将 $AI=BF=4$，$BJ=AF=10$ 代入解得 $FG=\frac{58}{7}$ 。因此$DF=2DG=2\sqrt{D{{F}^{2}}-F{{G}^{2}}}=2\sqrt{{{14}^{2}}-{{\left(\frac{58}{7} \right)}^{2}}}=\frac{8\sqrt{390}}{7}$ 。
故 $m+n+p=8+390+7=405$ 。
答案
解析
备注
