设 $O$ 是一个正八面体，$C$ 是一个正方体，且 $C$ 的各个顶点分别是 $O$ 每个面的中心。若 与 $C$ 的体积之比为 $\frac{m}{n}$，其中 $m$，$n$ 为互素的整数，试求 $m+n$ 。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
11
【解析】
如图所示，将正八面体放在空间直角坐标系中，由于正八面体棱长的长短不影响 $\frac{{{V}_{0}}}{{{V}_{c}}}$ 的比值，故可设正八面体的每个顶点都在坐标轴上，并且离原点的距离为1个单位长度。
正八面体 $O$ 上半部分是底面面积为 $\frac{1}{2}\times2\times 2=2$，高为1的正四棱锥，上半部分的体积为 $\frac{1}{3}\times1\times 2=\frac{2}{3}$，同理下半部分的体积也为 $\frac{2}{3}$，因此正八面体的体积为 $\frac{4}{3}$ 。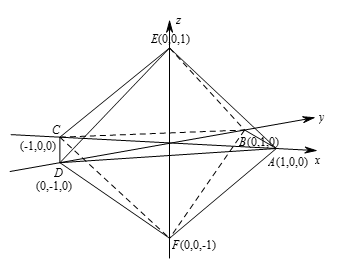
再来求立方体的体积，正八面体各个面中心的坐标是 $\left( \pm \frac{1}{3},\pm \frac{1}{3},\pm \frac{1}{3} \right)$，因此，正方体的棱长为 $\frac{2}{3}$，正方体的体积为 $\frac{2}{3}\times\frac{2}{3}\times \frac{2}{3}=\frac{8}{27}$ 。
所以 $\frac{{{V}_{0}}}{{{V}_{C}}}=\frac{9}{2}$，即 $m+n=9+2=11$ 。
正八面体 $O$ 上半部分是底面面积为 $\frac{1}{2}\times2\times 2=2$，高为1的正四棱锥，上半部分的体积为 $\frac{1}{3}\times1\times 2=\frac{2}{3}$，同理下半部分的体积也为 $\frac{2}{3}$，因此正八面体的体积为 $\frac{4}{3}$ 。
再来求立方体的体积，正八面体各个面中心的坐标是 $\left( \pm \frac{1}{3},\pm \frac{1}{3},\pm \frac{1}{3} \right)$，因此，正方体的棱长为 $\frac{2}{3}$，正方体的体积为 $\frac{2}{3}\times\frac{2}{3}\times \frac{2}{3}=\frac{8}{27}$ 。所以 $\frac{{{V}_{0}}}{{{V}_{C}}}=\frac{9}{2}$，即 $m+n=9+2=11$ 。
答案
解析
备注
