查看数据源：5c74ea93210b28428f14cc50
正方形 $ABCD$ 的中心为0，$AB=900$，点 $E$，$F$ 上，且 $AE<BF$，点 $E$ 在点 $A$，$F$ 之间，$\angle BOF={{45}^{\circ }}$，$EF=400$，设 $BF=p+q\sqrt{r}$，其中 $p$，$q$，$r$ 是正整数，$r$ 不能被任何素数的平方整除。试求 $p+q+r$ 。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
  • 知识点
    >
    数论初步
    >
    整除与同余
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的图象变换
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的对称性
【答案】
262
【解析】
运用复平面求解。
如图所示，设 $O$ 为原点，$AB$ 平行于 $x$ 轴，则 $A=450+450i$，$B=-450+450i$ 。点 $E$，$F$ 在线段 $AB$ 上，$\angle EOF={{45}^{\circ }}$，设 $E=x+450i\left( x\right)$，那么 $F=\left( x-400 \right)+450i$ 。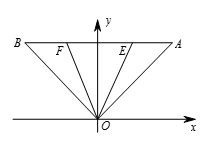另一方面，向量 $F$ 可由向量 $E$ 旋转 ${{45}^{\circ}}$ 得到，是向量 $E$ 的常数倍，因此 $F=c\left( 1+i\right)\left( x+450i \right)\left( c \right)$ 。
两个复数相等当且仅当它们的实部和虚部都分别相等，因此得到两个方程：
$\left\{ \begin{align}
& x-400=c\left( x-450 \right) \\
& 450=c\left( x+450 \right) \\
\end{align} \right.$
解关于 $x$ 的方程组，得 $\left( x-400\right)\left( x+450 \right)=450\left( x-450 \right)$，解得 $x=200\pm5\sqrt{7}$ 。因为 $AE<BF$，所以取 $x=200+5\sqrt{7}$，故 $E=\left(200+5\sqrt{7} \right)-450\text{i}$，$F=\left( -200+5\sqrt{7}\right)+450\text{i}$，所以 $\left| BF\right|=250+5\sqrt{7}$，因此 $p+q+r=250+5+7=262$ 。
【点评】在边 $BC$ 上一点 ${E}'$，使得 $B{E}'=AE$ 。易知 $\vartriangle AOE\cong \vartriangle BO{E}'$，故 $OE=O{E}'$，
$\angle EO{E}'=\angle AOB+\angle BO{E}'-\angle AOE=\angle AOE={{90}^{\circ }}$ 。 $\angle FO{E}'={{90}^{\circ }}-{{45}^{\circ }}={{45}^{\circ }}$ 。由 $OE=O{E}'$，$OF=OF$，$\angle FPE=\angle FP{E}'$ 知 $\Delta OEF\cong \Delta O{E}'F$，故 ${E}'F=EF=400$ 。
设 $BF=x$，那么 $B{E}'=AE=900-400-x=500-x$，由勾股定理得 ${{400}^{2}}={{\left(500-x \right)}^{2}}+{{x}^{2}}$，解得 $x=250+5\sqrt{7}$（因为 $AE<BF$，所以 $500-x<x$，即 $x>250$）。
因此 $p+q+r=250+5+7=262$ 。
答案 解析 备注
0.110299s