设 ${{\omega }_{1}}$,${{\omega }_{2}}$ 分别表示圆 ${{x}^{2}}+{{y}^{2}}+10x-24y-87=0$ 和圆 ${{x}^{2}}+{{y}^{2}}-10x-24y+153=0$,直线 $y=ax$ 经过某个内切于 ${{\omega }_{1}}$ 同时外切于 ${{\omega }_{2}}$ 的圆的圆心,设 $m$ 为 $a$ 的所有取值中最小正数,令 ${{m}^{2}}=\frac{p}{q}$,其中 $p$,$q$ 是互素的正整数,试求 $p+q$ 。
【难度】
【出处】
2005年第23届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
169
【解析】
如图所示,两圆的方程为 ${{\left( x+5\right)}^{2}}+{{\left( y-12 \right)}^{2}}={{16}^{2}}$ 和 ${{\left(x-5 \right)}^{2}}+{{\left( y-12 \right)}^{2}}={{4}^{2}}$,所以第一个圆半径为16,圆心为 $\left(-5 12 \right)$,第二个圆半径为4,圆心为 $\left(5 12 \right)$,内切于 ${{\omega }_{1}}$ 且外切于 ${{\omega}_{2}}$ 的第三个圆的圆心与化 ${{\omega }_{1}}$,${{\omega}_{2}}$ 圆心距离分别为 $16-r$,$r+4$ $\left(r \right)$ 。因为 $\left( 16-r \right)+\left( r+4\right)=20$ 是常量,因此第三个圆的圆心轨迹为一个椭圆,焦点为两圆圆心 $\left( -5 12\right)$ 与 $\left( 5 12 \right)$,长轴平行于 $x$ 轴,长度为20,椭圆圆心为 $\left(0 12 \right)$ 。椭圆的短轴长为 $\sqrt{{{20}^{2}}-{{\left(5-\left( -5 \right) \right)}^{2}}}=10\sqrt{3}$,因此椭圆的方程为 $\frac{{{x}^{2}}}{100}+\frac{{{\left(y-1 \right)}^{2}}}{75}=1$ 。消去分母,得 $3{{x}^{2}}+4{{\left(y-12 \right)}^{2}}=300$,将 $y=ax$ 代入方程,得到 $\left(3+4{{a}^{2}} \right){{x}^{2}}-96ax+276=0$ 。这个二次方程至少有一解当且仅当判别式非负,因此有不等式
$\left( {{96}^{2}} \right){{a}^{2}}-4\left(3+4{{a}^{2}} \right)\times 276\geqslant 0$
成立,整理得 $300{{a}^{2}}-207\geqslant 0$,${{a}^{2}}\geqslant\frac{69}{100}$ 。
因为 $m$ 为 $a$ 的所有取值中最小正数,因此 ${{m}^{2}}=\frac{69}{100}$,所以 $p+q=69+100=169$ 。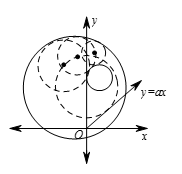
$\left( {{96}^{2}} \right){{a}^{2}}-4\left(3+4{{a}^{2}} \right)\times 276\geqslant 0$
成立,整理得 $300{{a}^{2}}-207\geqslant 0$,${{a}^{2}}\geqslant\frac{69}{100}$ 。
因为 $m$ 为 $a$ 的所有取值中最小正数,因此 ${{m}^{2}}=\frac{69}{100}$,所以 $p+q=69+100=169$ 。

答案
解析
备注