如图24-3所示,坐标平面第一象限内放置了8个直径为1的圆,定义 $R$ 为该8个圆组成的区域。斜率为3的直线 $l$ 将 $R$ 分成两相等的部分,其表达式为 $ax=by+c$,其中 $a$,$b$,$c$ 都是正整数且最大公约数为1。求 ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ 。

【难度】
【出处】
2006年第24届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
65
【解析】
首先注意到这样的直线是唯一的,如图所示,该设直线方程为 $y=3x+d$,则当直线与区域 $R$ 相交时,随着 $d$ 的减少,在直线上方的 $R$ 的部分的面积将严格递增,在直线下方的 $R$ 的部分的面积将严格递增,记最下面左边两个圆的对称点(即两圆的切点)为 $A$,则A的坐标为 $\left( 1,\frac{1}{2}\right)$,且任意经过点 $A$ 的直线将这两个圆分成面积相等的两部分。同理,任意经过点 $B$ 的直线将中间最上面的两个圆分成面积相等的两部分。剩下的四个圆,两两分别在直线 $AB$ 的两边。因而直线 $AB$ 将区域 $R$ 分成面积相等的两部分。由于直线 $AB$ 的斜率是3,所以直线 $AB$ 就是直线 $l$,它的方程是 $y-\frac{1}{2}=3\left( x-1\right)$,即 $6x=2y+5$,故 ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=36+4+25+65$ 。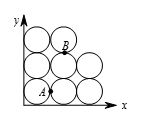

答案
解析
备注