凸六边形 $ABCDEF$ 所有边的长度都相等,$\angle A$ 和 $\angle D$ 是直角,其余各角都相等。若六边形的面积是 $2116\left( \sqrt{2}+1 \right)$,求边 $AB$ 的长。
【难度】
【出处】
2006年第24届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
46
【解析】
因为 $\angle B \angle C \angle E \angle F$ 都相等,故它们的度数都等于 $\frac{720-2.90}{4}=135$ 。如图所示,线段 $BF$ 和线段 $CE$ 把这个六边形分为两个直角三角形和一个矩形,设 $AB=x$,则 $BF=\sqrt{2x}$,从而
$2116\left(\sqrt{2}+1 \right)={{S}_{ABCDEF}}=2\cdot \frac{1}{2}{{x}^{2}}+x\cdot x\sqrt{2}$ 。
$=\left(\sqrt{2}+1 \right){{x}^{2}}$ 。
因此 ${{x}^{2}}=2116$,故 $x=46$ 。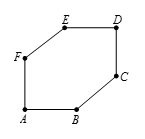
$2116\left(\sqrt{2}+1 \right)={{S}_{ABCDEF}}=2\cdot \frac{1}{2}{{x}^{2}}+x\cdot x\sqrt{2}$ 。
$=\left(\sqrt{2}+1 \right){{x}^{2}}$ 。
因此 ${{x}^{2}}=2116$,故 $x=46$ 。

答案
解析
备注