正方形就 $ABCD$ 的边长为1,点 $E F$ 分别在 $BC CD$ 边上,且 $\vartriangle AEF$ 是等边三角形。另有一小正方形以 $B$ 为顶点,各边分别与 $ABCD$ 的各边平行,且有一顶点在线段 $AE$ 上,若小正方形的边长为 $\frac{a-\sqrt{b}}{c}$,其中 $a b c$ 均为正整数,且 $b$ 不能被任何素数的平方整除。试求 $a+b+c$ 的值。
【难度】
【出处】
2006年第24届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
12
【解析】
如图所示,设小正方形为 $BOPQ$,其中点 $Q$ 在线段 $AB$ 上。设 $BQ=y$,则 $QP\text{=}y AQ=y\cdot\tan {{75}^{\circ }}$ 。因此 $1=AQ+QB=y\left( \tan {{75}^{\circ }}+1\right)=\left( 3+\sqrt{3} \right)y$,故 $y=\frac{1}{3\sqrt{3}}=\frac{3-\sqrt{3}}{6}$ 。因此 $a+b+c=12$ 。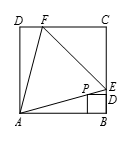

答案
解析
备注